>> Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний
§ 30 УРАВНЕНИЕ, ОПИСЫВАЮЩЕЕ ПРОЦЕССЫ В КОЛЕБАТЕЛЬНОМ КОНТУРЕ. ПЕРИОД СВОБОДНЫХ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ
Перейдем теперь к количественной теории процессов в колебательном контуре.
Уравнение, описывающее процессы в колебательном контуре. Рассмотрим колебательный контур, сопротивлением R которого можно пренебречь (рис. 4.6).
Уравнение, описываюндее свободные электрические колебания в контуре, можно получить с помощью закона сохранения энергии. Полная электромагнитная энергия W контура в любой момент времени равна сумме его энергий магнитного и электрического полей:
![]()
Эта энергия не меняется с течением времени, если ео противление R контура равно нулю. Значит, производная полной энергии по времени равна нулю. Следовательно, равна нулю сумма производных по времени от энергий магнитного и электрического полей:

Физический смысл уравнения (4.5) состоит в том, что скорость изменения энергии магнитного поля по модулю равна скорости изменения энергии электрического поля; знак «-» указывает на то, что, когда энергия электрического поля возрастает, энергия магнитного поля убывает (и наоборот).
Вычислив производные в уравнении (4.5), получим 1
Но производная заряда по времени представляет собой силу тока в данный момент времени:
Поэтому уравнение (4.6) можно переписать в следующем виде:
1 Мы вычисляем производные по времени. Поэтому производная (і 2)" равна не просто 2 і , как было бы при вычислении производной но і. Нужно 2 і умножить еще на производную i" силы тока по времени, так как вычисляется производная от сложной функции. То же самое относится к производной (q 2)".
Производная силы тока по времени есть не что иное, как вторая производная заряда по времени, подобно тому как производная скорости по времени (ускорение) есть вторая производная координаты по времени. Подставив в уравнение (4.8) і" = q" и разделив левую и правую части этого уравнения на Li, получим основное уравнение, описывающее свободные электрические колебания в контуре:

Теперь вы в полной мере можете оценить значение тех усилий, которые были затрачены для изучения колебаний шарика на пружине и математического маятника. Ведь уравнение (4.9) ничем, кроме обозначений, не отличается от уравнения (3.11), описывающего колебания шарика на пружине. При замене в уравнении (3.11) х на q, х" на q", k нa 1/C и m нa L мы в точности получим уравнение (4.9). Но уравнение (3.11) было уже решено выше. Поэтому, зная формулу, описывающую колебания пружинного маятника, мы сразу же можем записать формулу для описания электрических колебаний в контуре.
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки- Электромагнитные колебания – это периодические изменения со временем электрических и магнитных величин в электрической цепи.
- Свободными называются такие колебания , которые возникают в замкнутой системе вследствие отклонения этой системы от состояния устойчивого равновесия.
При колебаниях происходит непрерывный процесс превращения энергии системы из одной формы в другую. В случае колебаний электромагнитного поля обмен может идти только между электрической и магнитной составляющей этого поля. Простейшей системой, где может происходить этот процесс, является колебательный контур .
- Идеальный колебательный контур (LC-контур ) - электрическая цепь, состоящая из катушки индуктивностью L и конденсатора емкостью C .
В отличие от реального колебательного контура, который обладает электрическим сопротивлением R , электрическое сопротивление идеального контура всегда равна нулю. Следовательно, идеальный колебательный контур является упрощенной моделью реального контура.
На рисунке 1 изображена схема идеального колебательного контура.
Энергии контура
Полная энергия колебательного контура
\(W=W_{e} + W_{m}, \; \; \; W_{e} =\dfrac{C\cdot u^{2} }{2} = \dfrac{q^{2} }{2C}, \; \; \; W_{m} =\dfrac{L\cdot i^{2}}{2},\)
Где W e - энергия электрического поля колебательного контура в данный момент времени, С - электроемкость конденсатора, u - значение напряжения на конденсаторе в данный момент времени, q - значение заряда конденсатора в данный момент времени, W m - энергия магнитного поля колебательного контура в данный момент времени, L - индуктивность катушки, i -значение силы тока в катушке в данный момент времени.
Процессы в колебательном контуре
Рассмотрим процессы, которые возникают в колебательном контуре.
Для выведения контура из положения равновесия зарядим конденсатор так, что на его обкладках будет заряд Q m (рис. 2, положение 1 ). С учетом уравнения \(U_{m}=\dfrac{Q_{m}}{C}\) находим значение напряжения на конденсаторе. Тока в цепи в этом момент времени нет, т.е. i = 0.
После замыкания ключа под действием электрического поля конденсатора в цепи появится электрический ток, сила тока i которого будет увеличиваться с течением времени. Конденсатор в это время начнет разряжаться, т.к. электроны, создающие ток, (Напоминаю, что за направление тока принято направление движения положительных зарядов) уходят с отрицательной обкладки конденсатора и приходят на положительную (см. рис. 2, положение 2 ). Вместе с зарядом q будет уменьшаться и напряжение u \(\left(u = \dfrac{q}{C} \right).\) При увеличении силы тока через катушку возникнет ЭДС самоиндукции, препятствующая изменению силы тока. Вследствие этого, сила тока в колебательном контуре будет возрастать от нуля до некоторого максимального значения не мгновенно, а в течение некоторого промежутка времени, определяемого индуктивностью катушки.
Заряд конденсатора q уменьшается и в некоторый момент времени становится равным нулю (q = 0, u = 0), сила тока в катушке достигнет некоторого значения I m (см. рис. 2, положение 3 ).
Без электрического поля конденсатора (и сопротивления) электроны, создающие ток, продолжают свое движение по инерции. При этом электроны, приходящие на нейтральную обкладку конденсатора, сообщают ей отрицательный заряд, электроны, уходящие с нейтральной обкладки, сообщают ей положительный заряд. На конденсаторе начинает появляться заряд q (и напряжение u ), но противоположного знака, т.е. конденсатор перезаряжается. Теперь новое электрическое поле конденсатора препятствует движению электронов, поэтому сила тока i начинает убывать (см. рис. 2, положение 4 ). Опять же это происходит не мгновенно, поскольку теперь ЭДС самоиндукции стремится скомпенсировать уменьшение тока и «поддерживает» его. А значение силы тока I m (в положении 3 ) оказывается максимальным значением силы тока в контуре.
И снова под действием электрического поля конденсатора в цепи появится электрический ток, но направленный в противоположную сторону, сила тока i которого будет увеличиваться с течением времени. А конденсатор в это время будет разряжаться (см. рис. 2, положение 6 )до нуля (см. рис. 2, положение 7 ). И так далее.
Так как заряд на конденсаторе q (и напряжение u ) определяет его энергию электрического поля W e \(\left(W_{e}=\dfrac{q^{2}}{2C}=\dfrac{C \cdot u^{2}}{2} \right),\) а сила тока в катушке i - энергию магнитного поля Wm \(\left(W_{m}=\dfrac{L \cdot i^{2}}{2} \right),\) то вместе с изменениями заряда, напряжения и силы тока, будут изменяться и энергии.

Обозначения в таблице:
\(W_{e\, \max } =\dfrac{Q_{m}^{2} }{2C} =\dfrac{C\cdot U_{m}^{2} }{2}, \; \; \; W_{e\, 2} =\dfrac{q_{2}^{2} }{2C} =\dfrac{C\cdot u_{2}^{2} }{2}, \; \; \; W_{e\, 4} =\dfrac{q_{4}^{2} }{2C} =\dfrac{C\cdot u_{4}^{2} }{2}, \; \; \; W_{e\, 6} =\dfrac{q_{6}^{2} }{2C} =\dfrac{C\cdot u_{6}^{2} }{2},\)
\(W_{m\; \max } =\dfrac{L\cdot I_{m}^{2} }{2}, \; \; \; W_{m2} =\dfrac{L\cdot i_{2}^{2} }{2}, \; \; \; W_{m4} =\dfrac{L\cdot i_{4}^{2} }{2}, \; \; \; W_{m6} =\dfrac{L\cdot i_{6}^{2} }{2}.\)
Полная энергия идеального колебательного контура сохраняется с течением времени, поскольку в нем потерь энергии (нет сопротивления). Тогда
\(W=W_{e\, \max } = W_{m\, \max } = W_{e2} + W_{m2} = W_{e4} +W_{m4} = ...\)
Таким образом, в идеальном LC -контуре будут происходить периодические изменения значений силы тока i , заряда q и напряжения u , причем полная энергия контура при этом будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания .
- Свободные электромагнитные колебания в контуре - это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением ЭДС самоиндукции в катушке, которая «обеспечивает» эту перезарядку. Заметим, что заряд конденсатора q и сила тока в катушке i достигают своих максимальных значений Q m и I m в различные моменты времени.
Свободные электромагнитные колебания в контуре происходят по гармоническому закону:
\(q=Q_{m} \cdot \cos \left(\omega \cdot t+\varphi _{1} \right), \; \; \; u=U_{m} \cdot \cos \left(\omega \cdot t+\varphi _{1} \right), \; \; \; i=I_{m} \cdot \cos \left(\omega \cdot t+\varphi _{2} \right).\)
Наименьший промежуток времени, в течение которого LC -контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в LC -контуре определяется по формуле Томсона:
\(T=2\pi \cdot \sqrt{L\cdot C}, \;\;\; \omega =\dfrac{1}{\sqrt{L\cdot C}}.\)
Сточки зрения механической аналогии, идеальному колебательному контурусоответствует пружинный маятник без трения, а реальному - с трением. Вследствиедействия сил трения колебания пружинного маятника затухают с течением времени.
*Вывод формулы Томсона
Поскольку полная энергия идеального LC -контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
\(W=\dfrac{Q_{m}^{2} }{2C} =\dfrac{L\cdot I_{m}^{2} }{2} =\dfrac{q^{2} }{2C} +\dfrac{L\cdot i^{2} }{2} ={\rm const}.\)
Получим уравнение колебаний в LC -контуре, используя закон сохранения энергии. Продифференцировав выражение для его полной энергии по времени, с учетом того, что
\(W"=0, \;\;\; q"=i, \;\;\; i"=q"",\)
получаем уравнение, описывающее свободные колебания в идеальном контуре:
\(\left(\dfrac{q^{2} }{2C} +\dfrac{L\cdot i^{2} }{2} \right)^{{"} } =\dfrac{q}{C} \cdot q"+L\cdot i\cdot i" = \dfrac{q}{C} \cdot q"+L\cdot q"\cdot q""=0,\)
\(\dfrac{q}{C} +L\cdot q""=0,\; \; \; \; q""+\dfrac{1}{L\cdot C} \cdot q=0.\)
Переписав его в виде:
\(q""+\omega ^{2} \cdot q=0,\)
замечаем, что это - уравнение гармонических колебаний с циклической частотой
\(\omega =\dfrac{1}{\sqrt{L\cdot C} }.\)
Соответственно период рассматриваемых колебаний
\(T=\dfrac{2\pi }{\omega } =2\pi \cdot \sqrt{L\cdot C}.\)
Литература
- Жилко, В.В. Физика: учеб. пособие для 11 класса общеобразоват. шк. с рус. яз. обучения / В.В. Жилко, Л.Г. Маркович. - Минск: Нар. Асвета, 2009. - С. 39-43.
Урок № 48-169 Колебательный контур. Свободные электромагнитные колебания. Превращение энергии в колебательном контуре. Формула Томпсона. Колебания - движения или состояния, повторяющиеся во времени. Электромагнитные колебания - это колебания электрических и магнитных полей, которые сопро вождаются периодическим измене нием заряда, тока и напряжения. Колебательный контур - это система, состоящая из катушки индуктивности и конденсатора (рис. а). Если конденсатор зарядить и замкнуть на катушку, то по катушке потечет ток (рис. б). Когда конденсатор разрядится, ток в цепи не прекратится из-за самоиндукции в катушке. Индукционный ток, в соответствии с правилом Ленца, будет течь в ту же сторону и перезарядит конденсатор (рис. в). Ток в данном направлении прекратится, и процесс повторится в обратном направлении (рис. г).
Таким образом, в колеба
тельном контуре происхо
дят электромагнитные колеба
ния из-за превращения энергии
электрического поля конденсато
ра
( W Э = 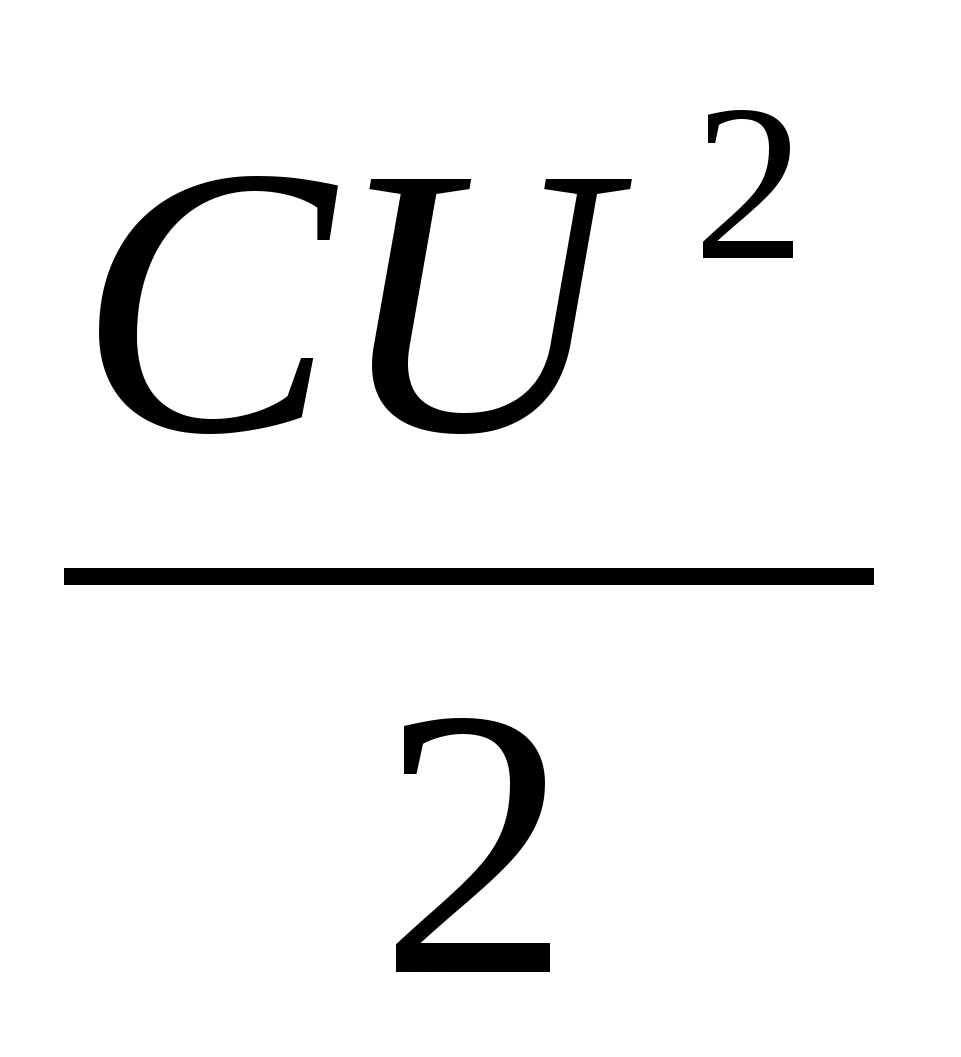 )
в энергию магнитного поля катушки с током
(W М =
)
в энергию магнитного поля катушки с током
(W М = ),
и наоборот
.
),
и наоборот
.
Гармонические колебания - периодические изменения физической величины в зависимости от времени, происходящие по закону синуса или косинуса.
 Уравнение, описывающее свободные электромагнитные колебания, принимает вид
Уравнение, описывающее свободные электромагнитные колебания, принимает вид
q"= - ω 0 2 q (q"- вторая производная.
Основные характеристики колебательного движения:
Период колебаний - минимальный промежуток времени Т, через который процесс полностью повторяется.
Амплитуда гармонических колебаний - модуль наибольшего значения колеблющейся величины.
Зная период, можно определить частоту колебаний, т. е. число колебаний в единицу времени, например в секунду. Если одно колебание совершается за время Т, то число колебаний за 1 с νопределяется так: ν = 1/Т.
Напомним, что в Международной системе единиц (СИ) частота колебаний равна единице, если за 1 с совершается одно колебание. Единица частоты называется герцем (сокращенно: Гц) в честь немецкого физика Генриха Ге р ц а.
Через промежуток времени, равный периоду Т,
т. е. при увеличении аргумента косинуса на ω 0
Т,
значение заряда повторяется и косинус принимает прежнее значение. Из курса математики известно, что наименьший период косинуса равен 2л. Следовательно, ω 0
Т
=2π,
откуда ω 0
=  =2πν Таким образом, величина ω 0
- это число колебаний, но не за 1 с, а за 2л с. Она называется циклической
или круговой частотой.
=2πν Таким образом, величина ω 0
- это число колебаний, но не за 1 с, а за 2л с. Она называется циклической
или круговой частотой.
Частоту свободных колебаний называют собственной частотой колебательной системы. Часто в дальнейшем для краткости мы будем называть циклическую частоту просто частотой. Отличить циклическую частоту ω 0 от частоты ν можно по обозначениям.
По аналогии с решением дифференциального уравнения для механической колебательной системы циклическая частота свободных электриче
ских колебаний
равна:ω 0 =
Период свободных колебаний в контуре равен: Т= =2π
=2π - формула Томсона.
- формула Томсона.
Фаза колебаний (от греческого слова phasis – появление, ступень развития какого-либо явления) – величина φ, стоящая под знаком косинуса или синуса. Выражается фаза в угловых единицах – радианах. Фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени.
Колебания с одинаковыми амплитудами и частотами могут отличаться друг от друга фазами.
Так как ω 0
= , то φ= ω 0
Т=2π
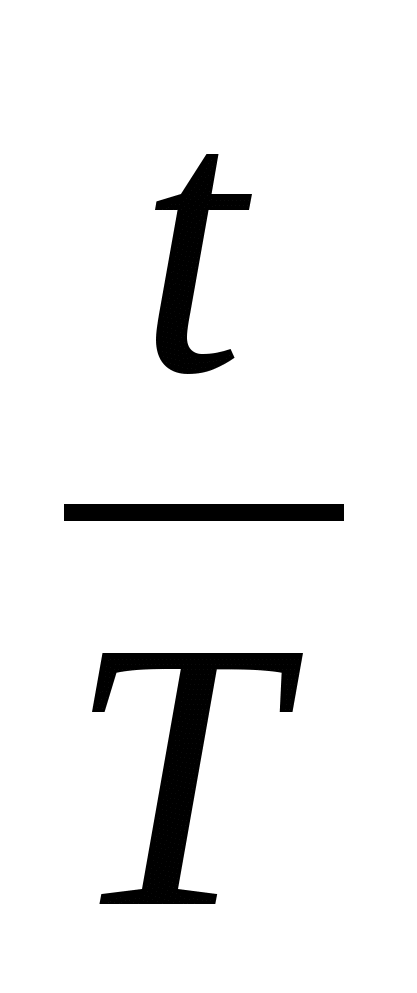 . Отношение показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. Так, по прошествии времени t=
. Отношение показывает, какая часть периода прошла от момента начала колебаний. Любому значению времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. Так, по прошествии времени t= (четверти периода) φ=
(четверти периода) φ= , по прошествии половины периода φ = π, по прошествии целого периода φ=2π и т.д.Можно изобразить на графике зависимость
, по прошествии половины периода φ = π, по прошествии целого периода φ=2π и т.д.Можно изобразить на графике зависимость
 заряда не от времени, а от фазы. На рисунке показана та же косинусоида, что и на предыдущем, но на горизонтальной оси отложены вместо времени
заряда не от времени, а от фазы. На рисунке показана та же косинусоида, что и на предыдущем, но на горизонтальной оси отложены вместо времени
различные значения фазы φ.
Соответствие между механическими и электрическими величинами в колебательных процессах
Механические величины
Задачи .942(932). Начальный заряд, сообщенный конденсатору колебательного контура, уменьшили в 2 раза. Во сколько раз изменились: а) амплитуда напряжения; б) амплитуда силы тока;
в) суммарная энергия электрического поля конденсатора и магнитного поля катушки?
943(933). При увеличении напряжения на конденсаторе колебательного контура на 20 В амплитуда силы тока увеличилась в 2 раза. Найти начальное напряжение.
945(935). Колебательный контур состоит из конденсатора емкостью С = 400 пФ и катушки индуктивностью L = 10 мГн. Найти амплитуду колебаний силы тока I т , если амплитуда колебаний напряжения U т = 500 В.
952(942). Через какое время (в долях периода t/T) на конденсаторе колебательного контура впервые будет заряд, равный половине амплитудного значения?
957(947). Катушку какой индуктивности надо включить в колебательный контур, чтобы при емкости конденсатора 50 пФ получить частоту свободных колебаний 10 МГц?
Колебательный контур. Период свободных колебаний.
1. После того как конденсатору колебательного контура был сообщён заряд q = 10 -5 Кл, в контуре возникли затухающие колебания. Какое количество теплоты выделится в контуре к тому времени, когда колебания в нём полностью затухнут? Ёмкость конденсатора С=0,01мкФ.
2. Колебательный контур состоит из конденсатора ёмкостью 400нФ и катушки индуктивностью 9мкГн. Каков период собственных колебаний контура?
3. Какую индуктивность надо включить в колебательный контур, чтобы при ёмкости 100пФ получить период собственных колебаний 2∙ 10 -6 с.
4. Сравнить жесткости пружин k1/k2 двух маятников с массами грузов соответственно 200г и 400г, если периоды их колебаний равны.
5. Под действием неподвижно висящего груза на пружине её удлинение было равно 6,4см. Затем груз оттянули и отпустили, вследствие чего он начал колебаться. Определить период этих колебаний.
6. К пружине подвесили груз, вывели его из положения равновесия и отпустили. Груз начал колебаться с периодом 0,5с. Определите удлинение пружины после прекращения колебаний. Массу пружины не учитывать.
7. За одно и то же время один математический маятник совершает 25 колебаний, а другой 15. Найти их длины, если один из них на 10см короче другого. 8. Колебательный контур состоит из конденсатора ёмкостью 10мФ и катушки индуктивности 100мГн. Найти амплитуду колебаний напряжения, если амплитуда колебаний силы тока 0,1А 9. Индуктивность катушки колебательного контура 0,5мГн. Требуется настроить этот контур на частоту 1МГц. Какова должна быть ёмкость конденсатора в этом контуре?Экзаменационные вопросы:
1. Какое из приведенных ниже выражений определяет период свободных колебаний в колебательном контуре? А.
; Б.  ; В.
; В. 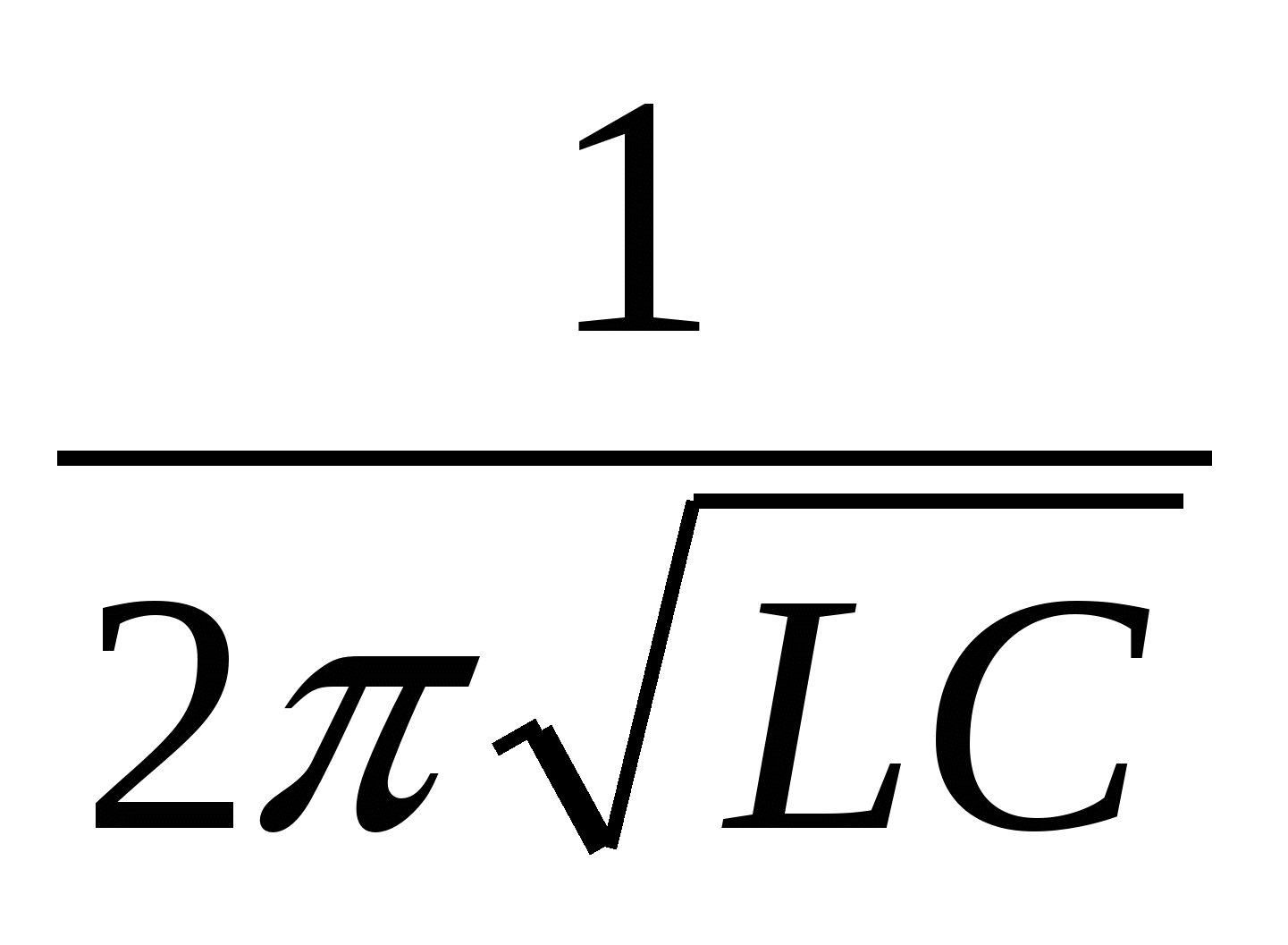 ; Г.
; Г.  ; Д. 2
.
; Д. 2
.
2 . Какое из приведенных ниже выражений определяет циклическую частоту свободных колебаний в колебательном контуре? А. Б.
. Какое из приведенных ниже выражений определяет циклическую частоту свободных колебаний в колебательном контуре? А. Б.  В.
В. 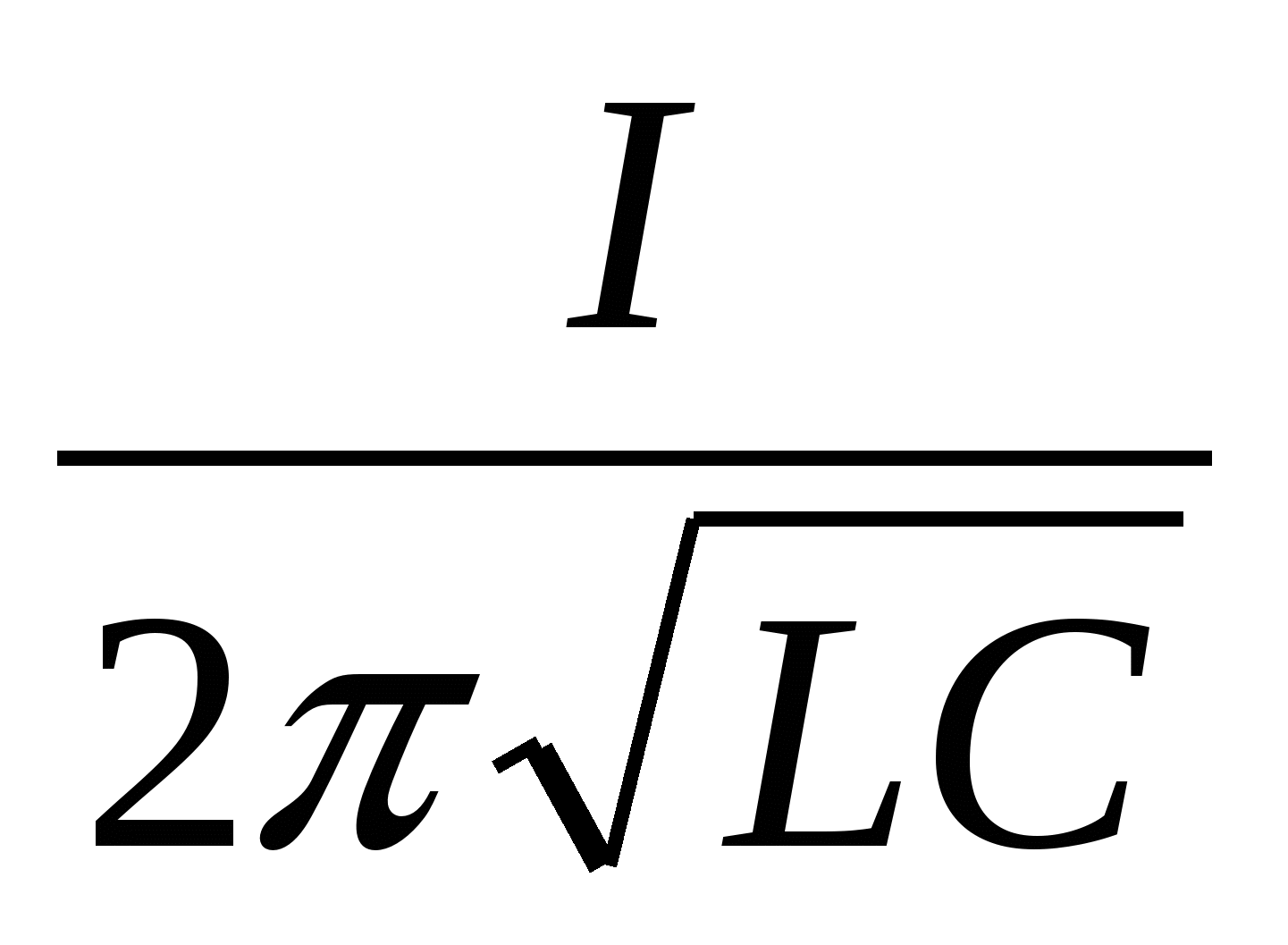 Г.
Г.  Д. 2π
Д. 2π
3. На рисунке представлен график зависимости координаты Х тела, совершающего гармонические колебания вдоль оси ох, от времени. Чему равен период колебания тела?
А. 1 с; Б. 2 с; В. 3 с. Г. 4 с.
4. На рисунке изображён профиль волны в определённый момент времени. Чему равна её длина?
А. 0,1 м. Б. 0,2 м. В. 2 м. Г. 4 м. Д. 5 м.5
 . На рисунке представлен график зависимости силы тока через катушку колебательного контура от времени. Чему равен период колебаний силы тока? А. 0,4 с. Б. 0,3 с. В. 0,2 с. Г. 0,1 с.
. На рисунке представлен график зависимости силы тока через катушку колебательного контура от времени. Чему равен период колебаний силы тока? А. 0,4 с. Б. 0,3 с. В. 0,2 с. Г. 0,1 с.
Д. Среди ответов А-Г нет правильного.

6. На рисунке изображён профиль волны в определённый момент времени. Чему равна её длина?
А. 0,2 м. Б. 0,4 м. В. 4 м. Г. 8 м. Д. 12 м.
7. Электрические колебания в колебательном контуре заданы уравнением q =10 -2 ∙ cos 20t (Кл).
Чему равна амплитуда колебаний заряда?
А . 10 -2 Кл. Б.cos 20t Кл. В.20t Кл. Г.20 Кл. Д.Среди ответов А-Г нет правильного.
8. При гармонических колебаниях вдоль оси ОХ координата тела изменяется по закону
X=0,2cos(5t+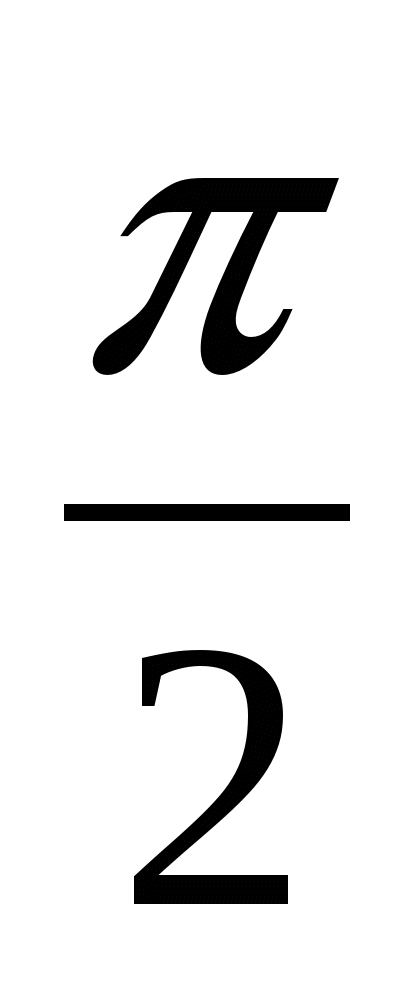 ). Чему равна амплитуда колебаний тела?
). Чему равна амплитуда колебаний тела?
А. Xм; Б. 0,2 м;В. сos(5t+) м; (5t+)м; Д.м
9. Частота колебаний источника волны 0,2 с -1 скорость распространения волны 10 м/с. Чему равна, длина волны? А. 0,02 м. Б. 2 м. В. 50 м.
Г. По условию задачи нельзя определить длину волны. Д. Среди ответов А-Г нет правильного.
10. Длина волны 40 м, скорость распространения 20 м/с. Чему равна частота колебаний источника волн?
А. 0,5 с -1 . Б. 2 с -1 . В. 800 с -1 .
Г. По условию задачи нельзя определить частоту колебания источника волн.
Д. Среди ответов А-Г нет правильного.
3
Свободные колебания в контуре.
Рассмотренные в предыдущих разделах цепи переменного тока наводят на мысль, что пара элементов − конденсатор и катушка индуктивности образуют своеобразную колебательную систему. Сейчас мы покажем, что это действительно так, в цепи состоящей только из этих элементов (рис. 669) возможны даже свободные колебания, то есть без внешнего источника ЭДС.
рис. 669
Поэтому цепь (или часть другой цепи), состоящая из конденсатора и катушки индуктивности называется колебательным контуром
.
Пусть конденсатор зарядили до заряда qo и затем подключили к нему катушку индуктивности. Такую процедуру легко осуществить с помощью цепи, схема которой показана на рис. 670: сначала ключ замыкают в положении 1
, при этом конденсатор заряжается до напряжения, равного ЭДС источника, после чего ключ перебрасывают в положения 2
, после чего начинается разрядка конденсатора через катушку.
рис. 670
Для определения зависимости заряда конденсатора от времени q(t)
применим закон Ома, согласно которому напряжение на конденсаторе U C = q/C
равно ЭДС самоиндукции, возникающей в катушке
здесь, «штрих» означает производную по времени.
Таким образом, оказывается справедливым уравнение
В этом уравнении содержится две неизвестных функции − зависимости от времени заряда q(t)
и силы тока I(t)
, поэтому его решить нельзя. Однако сила тока является производной от заряда конденсатора q / (t) = I(t)
, поэтому производная от силы тока является второй производной от заряда![]()
С учетом этого соотношения, перепишем уравнение (1) в виде
Поразительно, но это уравнение полностью совпадает с хорошо изученным нами уравнением гармонических колебаний (вторая производная от неизвестной функции пропорциональна самой этой функции с отрицательным коэффициентом пропорциональности x // = −ω o 2 x
)! Следовательно, решением этого уравнения будет гармоническая функция
с круговой частотой
Эта формула определяет собственную частоту колебательного контура
. Соответственно период колебаний заряда конденсатора (и силы тока в контуре) равен![]()
Полученное выражение для периода колебаний называется формулой Дж. Томпсона
.
Как обычно, для определения произвольных параметров A
, φ
в общем решении (4) необходимо задать начальные условия − заряд и силу тока в начальный момент времени. В частности, для рассмотренного примера цепи рис. 670, начальные условия имеют вид: при t = 0
, q = q o
, I = 0
, поэтому зависимость заряда конденсатора от времени будет описываться функцией
а сила тока изменяется со временем по закону
Приведенное рассмотрение колебательного контура является приближенным − любой реальный контур обладает активным сопротивлением (соединительных проводов и обмотки катушки).
рис. 671
Поэтому в уравнении (1) следует учесть падение напряжения на этом активном сопротивлении, поэтому это уравнение приобретет вид![]()
который с учетом связи между зарядом и силой тока, преобразуется к форме
Это уравнение нам также знакомо – это уравнение затухающих колебаний![]()
причем коэффициент затухания, как и следовало ожидать, пропорционален активному сопротивлению цепи β = R/L
.
Процессы, происходящие в колебательном контуре, могут быть также описаны и с помощью закона сохранения энергии. Если пренебречь активным сопротивлением контура, то сумма энергий электрического поля конденсатора и магнитного поля катушки остается постоянной, что выражается уравнением
которое также является уравнением гармонических колебаний с частотой, определяемой формулой (5). По свое форме это уравнение также совпадает уравнениями, следующими из закона сохранения энергии при механических колебаниях. Так как, уравнения, описывающие колебания электрического заряда конденсатора, аналогичны уравнениям, описывающим механические колебания, то можно провести аналогию между процессами, протекающими в колебательном контуре, и процессами в любой механической системе. На рис. 672 такая аналогия проведена для колебаний математического маятника. В этом случае аналогами являются «заряд конденсатора q(t)
− угол отклонения маятника φ(t)
» и «сила тока I(t) = q / (t)
− скорость движения маятника V(t)
».
рис. 672
Пользуясь этой аналогией, качественно опишем процесс колебаний заряда и электрического тока в контуре. В начальный момент времени конденсатор заряжен, сила электрического тока равна нулю, вся энергия заключена в энергии электрического поля конденсатора (что аналогично максимальному отклонения маятника от положения равновесия). Затем конденсатор начинает разряжаться, сила тока возрастает, при этом в катушке возникает ЭДС самоиндукции, которая препятствует возрастанию тока; энергия конденсатора уменьшается, переходя в энергию магнитного поля катушки (аналогия – маятник движется к нижней точки с возрастанием скорости движения). Когда заряд на конденсаторе становится равным нулю, сила тока достигает максимального значения, при этом вся энергия превращается в энергию магнитного поля (маятник достиг нижней точки, скорость его максимальна). Затем магнитное поле начинает убывать, при этом ЭДС самоиндукции поддерживает ток в прежнем направлении, при этом конденсатор начинает заряжаться, причем знаки зарядов на обкладках конденсатора противоположны начальному распределению (аналог − маятник движется к противоположному начальному максимальному отклонению). Затем ток в цепи прекращается, при этом заряд конденсатора становится опять максимальным, но противоположным по знаку (маятник достиг максимального отклонения), после чего процесс повторятся в противоположном направлении.
Электрический колебательный контур это система для возбуждения и поддержания электромагнитных колебаний. В простейшем виде это цепь, состоящая из включенных последовательно катушки индуктивностью L, конденсатора ёмкостью С и резистора сопротивлением R (рис.129). Когда переключатель П установлен в положении 1, происходит зарядка конденсатора С до напряжения U т . При этом между пластинами конденсатора образуется электрическое поле, максимальная энергия которого равна
При переводе
переключателя в положение 2 контур
замыкается и в нём протекают следующие
процессы. Конденсатор начинает разряжаться
и по цепи пойдёт ток i
,
величина
которого возрастает от нуля до
максимального значения
 ,
а затем снова уменьшается до нуля. Так
как в цепи протекает переменный по
величине ток, то в катушке индуцируется
ЭДС, которая препятствует разрядке
конденсатора. Поэтому процесс разрядки
конденсатора происходит не мгновенно,
а постепенно. В результате появления
тока в катушке возникает магнитное
поле, энергия которого
,
а затем снова уменьшается до нуля. Так
как в цепи протекает переменный по
величине ток, то в катушке индуцируется
ЭДС, которая препятствует разрядке
конденсатора. Поэтому процесс разрядки
конденсатора происходит не мгновенно,
а постепенно. В результате появления
тока в катушке возникает магнитное
поле, энергия которого достигает максимального значения при
токе равном
достигает максимального значения при
токе равном .
Максимальная энергия магнитного поля
будет равна
.
Максимальная энергия магнитного поля
будет равна

После достижения
максимального значения ток в контуре
начнёт убывать. При этом будет происходить
перезаряда конденсатора, энергия
магнитного поля в катушке будет убывать,
а энергия электрического поля в
конденсаторе возрастать. По достижении
максимального значения. Процесс начнёт
повторяться и в контуре происходят
колебания электрического и магнитного
полей. Если считать, что сопротивление
 (т.е. энергия на нагревание не расходуется),
то по закону сохранения энергии полная
энергияW
остаётся постоянной
(т.е. энергия на нагревание не расходуется),
то по закону сохранения энергии полная
энергияW
остаётся постоянной

и
 ;
; .
.
Контур, в котором не происходит потерь энергии, называется идеальным. Напряжение и ток в контуре изменяются по гармоническому закону
 ;
;

где
 - круговая (циклическая) частота колебаний
- круговая (циклическая) частота колебаний .
.
Круговая частота
связана с частотой колебаний
 и периодам колебаний Т соотношении.
и периодам колебаний Т соотношении.
Н а
рис. 130 представлены графики изменения
напряженияU
и тока I
в катушке идеального колебательного
контура. Видно, что сила тока отстаёт
по фазе от напряжения на
а
рис. 130 представлены графики изменения
напряженияU
и тока I
в катушке идеального колебательного
контура. Видно, что сила тока отстаёт
по фазе от напряжения на
 .
.
 ;
;
 ;
; - формула Томсона.
- формула Томсона.
В том случае, когда
сопротивление
 ,
формула Томсона принимает вид
,
формула Томсона принимает вид
 .
.
Основы теории Максвелла
Теорией Максвелла называется теория единого электромагнитного поля, создаваемого произвольной системой зарядов и токов. В теории решается основная задача электродинамики – по заданному распределению зарядов и токов отыскиваются характеристики создаваемых ими электрического и магнитного полей. Теория Максвелла является обобщением важнейших законов, описывающих электрические и электромагнитные явления – теоремы Остроградского-Гаусса для электрического и магнитного полей, закона полного тока, закона электромагнитной индукции и теоремы о циркуляции вектора напряженности электрического поля. Теория Максвелла носит феноменологический характер, т.е. в ней не рассматриваются внутренний механизм явлений, происходящих в среде и вызывающих появление электрического и магнитного полей. В теории Максвелла среда описывается с помощью трех характеристик – диэлектрической ε и магнитной μ проницаемостями среды и удельной электропроводностью γ.