Objectifs de la leçon:

Développer les connaissances, les compétences et les capacités pour utiliser efficacement la méthode généralisée des intervalles, basée sur la propriété des fonctions continues ;

Formuler un algorithme d'actions conduisant à des transformations équivalentes ;

Apprenez à l'appliquer de manière indépendante lors de la résolution d'inégalités ;

Transférer les connaissances, les compétences et les capacités vers de nouvelles conditions.

Pédagogique : systématisation, consolidation, généralisation des connaissances, compétences et aptitudes.

Éducatif : nourrir le besoin d’une argumentation cohérente, d’exactitude et d’indépendance à part entière.

Développemental : développement de la logique mathématique, formation d'un style de pensée mathématique (dissection claire du cours du raisonnement), intérêt cognitif.

1) Introduction, définition des buts et objectifs de la leçon - 2 min.

2) Vérification des devoirs - 2 min. (travail frontal, maîtrise de soi).

3) Justification mathématique des étapes de résolution des inégalités par la méthode des intervalles - 4 minutes (réponses préparées des élèves).

4) Répétition des propriétés des inégalités – 2 min.

5) Préparation à la maîtrise (étude) d'un nouveau matériel pédagogique par la répétition et la mise à jour des connaissances de base – 5 min. (travail de front, réponses aux questions, situations problématiques).

6) Méthode des intervalles généralisés pour résoudre les inégalités, compréhension initiale – 13 min. (solution collective des inégalités par la méthode des intervalles : au tableau et dans les cahiers).

7) Informations sur les devoirs, instructions pour les compléter – 1 min.

8) Consolidation des nouvelles connaissances – 15 min. (travail indépendant - option 1).

9) Résumer la leçon, réflexion – 1 min.

1) Introduction, fixant les buts et objectifs de la leçon. (Histoire du professeur)

1) La nécessité d'une utilisation plus large de la méthode des intervalles à l'école est dictée par l'idéologie de l'ensemble du processus d'enseignement des mathématiques. Le fait est que la ligne fonctionnelle (l'une des principales lors de l'étude des principes fondamentaux des mathématiques) reçoit un puissant support technologique. La méthode des intervalles est basée sur des caractéristiques de dépendance fonctionnelle aussi importantes que les zéros de la fonction, les intervalles de son signe constant et sa monotonie. L’origine fonctionnelle des équations et des inégalités, ainsi que les méthodes permettant de les résoudre, deviennent alors plus claires. Les catégories de continuité d'une fonction, le comportement de son graphe au voisinage de points de discontinuité infinie, les théorèmes sur les racines, la constance de signe, les points extrêmes et leurs types s'éclairent. Et tout cela est organiquement lié en un tout fonctionnel.

D'autre part, la géométrisation des objets de recherche utilisés est également inestimable, c'est-à-dire représenter visuellement et figurativement tous les outils mathématiques de dépendance fonctionnelle utilisés.

Les principes de base qui sous-tendent la méthode des intervalles :

• approche fonctionnelle (généralisée);
• le recours à la géométrisation des propriétés fonctionnelles ;
• visualisation de la recherche.

Cela conduit aux avantages suivants de la méthode par rapport à d'autres utilisées dans le même type de tâches : simplicité et rapidité d'atteinte de l'objectif ; la visibilité (et la capacité de contrôler ou de revérifier) ; économie de ressources et de temps informatiques ; l'étendue de la couverture de l'ensemble de la situation, la formation et le développement de compétences de pensée et d'analyse généralisées, ainsi que la capacité associée à tirer des conclusions logiques.

2) Vérification des devoirs.(Diapositive n°4)

3) Une histoire sur la méthode des intervalles pour résoudre les inégalités. (Réponses des élèves).

Justification mathématique pour résoudre les inégalités à l'aide de la méthode des intervalles.

1) Considérons les inégalités : (x-2)(x-3)>0. (diapositive numéro 5)

Vous pouvez le résoudre de cette façon : Le produit (quotient) de deux facteurs est positif si et seulement si les deux facteurs sont du même signe, c'est-à-dire l'inégalité équivaut à la combinaison de deux systèmes : (diapositive n°6)

Du premier système on obtient x >3, du second x< 2.

La solution est de combiner les solutions des deux systèmes.

Répondre:

Méthode graphique (diapositive numéro 7)

Une autre méthode est méthode d'intervalle(diapositive numéro 8).

Son idée est la suivante.

Marquons sur la droite numérique les zéros (racines) du polynôme (x-2)(x-3) debout

du côté gauche de l’inégalité, c’est-à-dire numéros 2 et 3.

Lorsque x >3 (à droite de la plus grande racine), alors (x-2)(x-3)>0, puisque chaque facteur est positif.

Si vous vous déplacez le long de l'axe dans une direction négative, alors en passant par le point x=3, le facteur (x-3) changera de signe. Dans le produit (x-2)(x-3) un facteur négatif apparaîtra, ce qui donnera (x-2)(x-3)<0. При переходе через следующий корень появится еще один отрицательный множитель и произведение (х-2)(х-3)>0.

Il est maintenant facile d’écrire la solution de l’inégalité :

Conclusion : le produit ne peut changer de signe qu'en passant par les points x=2 et x=3

et, par conséquent, préserve le signe sur chacun des intervalles résultants.

À partir de cet exemple simple, il est facile de comprendre l'idée de la méthode des intervalles, mais il ne montre pas ses avantages significatifs.

Considérons la rationalité de la méthode des intervalles et sa puissance dans l'exemple suivant (diapositive n° 9, 10,11, 12))

2) Résoudre l'inégalité (x-1)(x-2)(x-3)(x-4)(x-5)(x-6)(x-7)(x-8)(x-9) (x-10)>0.

Pour résoudre cette inégalité à l’aide d’un ensemble de systèmes, il faudrait considérer un ensemble de 512 systèmes avec 10 inégalités dans chaque système.

Utilisons la méthode des intervalles. Marquons les zéros du polynôme sur la droite numérique. Sur l'intervalle x>10 le polynôme sera positif, puisque chaque facteur est positif. En passant par chaque racine suivante, le polynôme changera de signe, puisqu'un facteur négatif supplémentaire apparaîtra dans le produit. Il est désormais facile d’écrire la solution de l’inégalité en utilisant des signes alternés.

Avantages de la méthode des intervalles.

• simplicité et rapidité pour atteindre l'objectif ;
• la visibilité (et la capacité de contrôler ou de revérifier) ;
• réduction significative de la quantité de travail et du temps de calcul ;
• l'étendue de la couverture de l'ensemble de la situation ;
• formation et développement de compétences de pensée et d'analyse généralisées, ainsi que la capacité associée à tirer des conclusions logiques.

Commentaire. Il est très pratique de résoudre des inégalités dont le côté gauche est factorisé, car il n'est pas difficile de trouver les zéros (racines).

Devoir : Résoudre l'inégalité à l'aide de la méthode des intervalles (x+3) 3 (x-4) 2 (x-5)>0(Diapositive 13)

4) Répétition des propriétés des inégalités.

a) Question : Quelles inégalités sont dites équivalentes ?

(Deux inégalités sont dites équivalentes si toute solution à la première inégalité est une solution à la seconde et, inversement, toute solution à la seconde est une solution à la première).

Ou : deux inégalités sont dites équivalentes si les ensembles de leurs solutions coïncident.

Diapositive 14. Répétition des propriétés des inégalités.

Diapositive 15. Répondez à la question et expliquez.

Les inégalités sont-elles équivalentes ?

1) 4x-5<0 и 4х<5

2) -2x+5>0 et 2x-5<0

3) -3x 2 +5x-7>0 et 3x 2 -5x+7<0

4) (x+1)>0 et (x 2 +5x+10)(x+1)>0

5) Travail oral frontal pour préparer l'assimilation (étude) de nouveau matériel pédagogique par la répétition et la mise à jour des connaissances de base.

Diapositive 16. Définition d'une fonction continue en un point.

Diapositive 17. Propriété des fonctions continues.

Diapositive 18. Trouvez des intervalles de continuité.

Diapositive 19. Trouvez l'erreur.

Diapositive 20. Résolvez l'inégalité oralement,
à l'aide d'un tableau.

Diapositive 21, 22. Remplacer l'inégalité par une condition équivalente.

Résoudre les inégalités

Cette inégalité est équivalente à la condition f(x) < 0, en comptant

Par conséquent, nous devons trouver toutes les valeurs de x pour lesquelles la condition f(x) est satisfaite < 0.

6) Méthode généralisée des intervalles pour résoudre les inégalités, compréhension initiale – 10 min. (solution collective des inégalités par la méthode des intervalles : au tableau et dans les cahiers).

Diapositive 23. Algorithme. Méthode généralisée de résolution des inégalités.

Résoudre les inégalités f(x)>0, f(x) > 0, f(x)<0, f(x)< 0 par méthode d'intervalle. (Schème)

Diapositives 24 et 25. Résoudre les inégalités à l'aide d'un algorithme. (Commentaires sur tous les points de l'algorithme).

Diapositive 26. Illustration graphique de la solution à cette inégalité.

Diapositive 27. Résoudre les inégalités au tableau et dans les cahiers .

Diapositive 28. Illustration graphique de la solution à cette inégalité.

Diapositive 29. Résoudre les inégalités au tableau et dans les cahiers

Diapositive 30. Illustration graphique de la solution à cette inégalité.

Diapositive 31, 32. Résolvez l'inégalité oralement, à l'aide d'une image

7) Informations sur les devoirs.(Résoudre par méthode d'intervalle option n°2)

8) Consolidation des nouvelles connaissances (travail indépendant, option n°1).

9) Résumer la leçon, maîtrise de soi à l'aide de solutions toutes faites (diapositives 33, 34, 35), répéter l'algorithme de la méthode des intervalles généralisés et son application.

10) Analyse des apprentissages des étudiants et de leur intérêt pour le sujet. Cette méthode est universelle pour résoudre toutes les inégalités, notamment rationnelles, de module, irrationnelles, exponentielles, logarithmiques, puisque la méthode des intervalles réduit la solution des inégalités à la solution d'équations ; trouver le domaine de définition et la valeur d'une fonction en un point ne pose pas de difficultés. Mais j'ai dû donner des exemples d'inégalités où l'utilisation de cette méthode n'est pas justifiée, où il est plus rationnel d'utiliser d'autres méthodes pour résoudre les inégalités.

Présentation « Application de la continuité dans la résolution des inégalités ». (35 diapositives)

Continuité de fonction. Points de rupture.

Le taureau marche, se balance, soupire en marchant :
- Oh, la planche s'épuise, maintenant je vais tomber !

Dans cette leçon, nous examinerons le concept de continuité d'une fonction, la classification des points de discontinuité et un problème pratique courant études de continuité des fonctions. D'après le nom même du sujet, beaucoup devinent intuitivement ce qui sera discuté et pensent que le matériel est assez simple. C'est vrai. Mais ce sont les tâches simples qui sont le plus souvent punies pour négligence et approche superficielle de leur résolution. Par conséquent, je vous recommande d'étudier l'article très attentivement et d'en saisir toutes les subtilités et techniques.

Que faut-il savoir et pouvoir faire ? Pas beaucoup. Pour bien apprendre la leçon, il faut comprendre de quoi il s'agit limite d'une fonction. Pour les lecteurs ayant un faible niveau de préparation, il suffit de comprendre l'article Limites de fonction. Exemples de solutions et regardez la signification géométrique de la limite dans le manuel Graphiques et propriétés des fonctions élémentaires. Il est également conseillé de se familiariser avec transformations géométriques de graphiques, puisque la pratique consiste dans la plupart des cas à construire un dessin. Les perspectives sont optimistes pour tout le monde, et même une bouilloire pleine sera capable de faire face seule à la tâche dans une heure ou deux !

Continuité de fonction. Points d'arrêt et leur classification

Notion de continuité de fonction

Considérons une fonction continue sur toute la droite numérique :

Ou, pour le dire plus succinctement, notre fonction est continue sur (l'ensemble des nombres réels).

Quel est le critère « philistin » de continuité ? Évidemment, le graphique d’une fonction continue peut être tracé sans retirer le crayon du papier.

Dans ce cas, deux notions simples doivent être clairement distinguées : domaine d'une fonction Et continuité de fonction. En général ce n'est pas la même chose. Par exemple:

Cette fonction est définie sur toute la droite numérique, c'est-à-dire pour tout le monde La signification de « x » a sa propre signification de « y ». En particulier, si , alors . A noter que l'autre point est ponctué, car par la définition d'une fonction, la valeur de l'argument doit correspondre à la seule chose valeur de la fonction. Ainsi, domaine notre fonction : .

Cependant cette fonction n'est pas activée en continu ! Il est bien évident qu'au moment où elle souffre écart. Le terme est également tout à fait intelligible et visuel ; en effet, ici, il faudra de toute façon arracher le crayon du papier. Un peu plus tard, nous examinerons la classification des points d'arrêt.

Continuité d'une fonction en un point et sur un intervalle

Dans un problème mathématique particulier, on peut parler de continuité d'une fonction en un point, de continuité d'une fonction sur un intervalle, un demi-intervalle, ou encore de continuité d'une fonction sur un segment. C'est, il n’y a pas de « simple continuité »– la fonction peut être continue QUELQUE PART. Et la « pierre angulaire » fondamentale de tout le reste est continuité de fonction à ce point .

La théorie de l'analyse mathématique donne une définition de la continuité d'une fonction en un point en utilisant les voisinages « delta » et « epsilon », mais en pratique il existe une définition différente en usage, à laquelle nous porterons une attention particulière.

Rappelons-nous d'abord limites unilatérales qui a fait irruption dans nos vies dès la première leçon à propos des graphiques de fonctions. Considérons une situation quotidienne :

Si l'on s'approche de l'axe jusqu'au point gauche(flèche rouge), puis les valeurs correspondantes des « jeux » iront le long de l'axe jusqu'au point (flèche cramoisie). Mathématiquement, ce fait est corrigé en utilisant limite à gauche:

Faites attention à l'entrée (lit "x tend vers ka à gauche"). L'« additif » « moins zéro » symbolise , cela signifie essentiellement que nous approchons du nombre du côté gauche.

De même, si vous approchez du point « ka » sur la droite(flèche bleue), alors les « jeux » auront la même valeur, mais le long de la flèche verte, et limite à droite sera formaté comme suit :

"Additif" symbolise , et l'entrée se lit comme suit : "x tend vers ka à droite."

Si les limites unilatérales sont finies et égales(comme dans notre cas) : , alors nous dirons qu'il existe une limite GÉNÉRALE. C'est simple, la limite générale est notre « habituelle » limite d'une fonction, égal à un nombre fini.

Notez que si la fonction n'est pas définie en (faites ressortir le point noir sur la branche du graphique), alors les calculs ci-dessus restent valables. Comme cela a déjà été souligné à plusieurs reprises, notamment dans l'article sur les fonctions infinitésimales, les expressions signifient que "x" infiniment proche aborde le sujet, tandis que N'IMPORTE PAS, que la fonction elle-même soit définie à un moment donné ou non. Un bon exemple sera trouvé dans le paragraphe suivant, lorsque la fonction sera analysée.

Définition: une fonction est continue en un point si la limite de la fonction en un point donné est égale à la valeur de la fonction en ce point : .

La définition est détaillée dans les termes suivants :

1) La fonction doit être définie au point, c'est-à-dire que la valeur doit exister.

2) Il doit y avoir une limite générale de la fonction. Comme indiqué ci-dessus, cela implique l'existence et l'égalité de limites unilatérales : .

3) La limite de la fonction en un point donné doit être égale à la valeur de la fonction en ce point : .

En cas de violation au moins un des trois conditions, alors la fonction perd la propriété de continuité au point .

Continuité d'une fonction sur un intervalle est formulée ingénieusement et très simplement : une fonction est continue sur l'intervalle si elle est continue en tout point de l'intervalle donné.

En particulier, de nombreuses fonctions sont continues sur un intervalle infini, c'est-à-dire sur l'ensemble des nombres réels. Il s'agit d'une fonction linéaire, polynômes, exponentielle, sinus, cosinus, etc. Et en général, tout fonction élémentaire continu sur son domaine de définition, par exemple, une fonction logarithmique est continue sur l'intervalle . J'espère que vous avez maintenant une assez bonne idée de ce à quoi ressemblent les graphiques des fonctions de base. Des informations plus détaillées sur leur continuité peuvent être obtenues auprès d'un homme aimable nommé Fichtenholtz.

Avec la continuité d'une fonction sur un segment et des demi-intervalles, tout n'est pas non plus difficile, mais il est plus approprié d'en parler en classe sur la recherche des valeurs minimales et maximales d'une fonction sur un segment, mais pour l’instant ne nous en inquiétons pas.

Classement des points de rupture

La vie passionnante des fonctions est riche de toutes sortes de particularités, et les points d'arrêt ne sont qu'une des pages de leur biographie.

Note : au cas où, je m'attarderai sur un point élémentaire : le point de rupture est toujours point unique– il n’y a pas de « plusieurs points de rupture d’affilée », c’est-à-dire qu’il n’existe pas d’« intervalle de pause ».

Ces points, à leur tour, sont divisés en deux grands groupes : ruptures du premier type Et ruptures du deuxième type. Chaque type d'écart a ses propres caractéristiques, que nous allons examiner tout de suite :

Point de discontinuité du premier type

Si la condition de continuité est violée en un point et limites unilatérales fini , alors on l'appelle point de discontinuité du premier type.

Commençons par le cas le plus optimiste. Selon l'idée originale de la leçon, je voulais raconter la théorie « en termes généraux », mais afin de démontrer la réalité de la matière, j'ai opté pour l'option avec des personnages spécifiques.

C'est triste, comme une photo de jeunes mariés sur fond de Flamme éternelle, mais le plan suivant est généralement accepté. Représentons le graphique de la fonction dans le dessin :


Cette fonction est continue sur toute la droite numérique, à l’exception du point. Et en fait, le dénominateur ne peut pas être égal à zéro. Cependant, conformément au sens de la limite, on peut infiniment proche approchez-vous de « zéro » à la fois par la gauche et par la droite, c'est-à-dire que des limites unilatérales existent et coïncident évidemment :
(La condition n°2 de continuité est satisfaite).

Mais la fonction n'est pas définie à ce point, par conséquent, la condition n° 1 de continuité est violée et la fonction souffre d'une discontinuité à ce point.

Une rupture de ce type (avec l'existant limite générale) sont appelés espace réparable. Pourquoi amovible ? Parce que la fonction peut redéfinir au point de rupture :

Est-ce que ça a l'air bizarre ? Peut être. Mais une telle notation de fonction ne contredit rien ! Maintenant, l'écart est comblé et tout le monde est content :


Effectuons un contrôle formel :

2) – il existe une limite générale ;
3)

Ainsi, les trois conditions sont satisfaites et la fonction est continue en un point par la définition de continuité d'une fonction en un point.

Cependant, les détracteurs du matan peuvent mal définir la fonction, par exemple :


Il est intéressant de noter que les deux premières conditions de continuité sont ici satisfaites :
1) – la fonction est définie en un point donné ;
2) – il existe une limite générale.

Mais la troisième frontière n'a pas été franchie : , c'est-à-dire la limite de la fonction au point inégal la valeur d'une fonction donnée en un point donné.

Ainsi, à un moment donné, la fonction subit une discontinuité.

Le deuxième cas, plus triste, s'appelle rupture du premier type avec un saut. Et la tristesse est évoquée par des limites unilatérales qui fini et différent. Un exemple est montré dans le deuxième dessin de la leçon. Un tel écart se produit généralement dans fonctions définies par morceaux, qui ont déjà été mentionnés dans l'article à propos des transformations graphiques.

Considérons la fonction par morceaux et nous terminerons son dessin. Comment construire un graphique ? Très simple. Sur un demi-intervalle, nous dessinons un fragment de parabole (vert), sur un intervalle - un segment de droite (rouge) et sur un demi-intervalle - une ligne droite (bleue).

De plus, en raison de l'inégalité, la valeur est déterminée pour la fonction quadratique (point vert), et en raison de l'inégalité, la valeur est déterminée pour la fonction linéaire (point bleu) :

Dans le cas le plus difficile, il faudra recourir à une construction point par point de chaque élément du graphique (voir le premier leçon sur les graphiques de fonctions).

Maintenant, nous ne nous intéresserons qu'au point. Examinons-le pour la continuité :

2) Calculons les limites unilatérales.

Sur la gauche, nous avons un segment de ligne rouge, donc la limite du côté gauche est :

A droite se trouve la droite bleue, et la limite de droite :

En conséquence, nous avons reçu nombres finis, et ils inégal. Depuis les limites unilatérales fini et différent: , alors notre fonction tolère discontinuité du premier type avec saut.

Il est logique que l'écart ne puisse pas être éliminé - la fonction ne peut vraiment pas être définie davantage et « collée ensemble », comme dans l'exemple précédent.

Points de discontinuité du deuxième type

Habituellement, tous les autres cas de rupture sont judicieusement classés dans cette catégorie. Je ne vais pas tout énumérer, car en pratique, dans 99% des problèmes que vous rencontrerez écart sans fin– qu’on soit gaucher ou droitier, et le plus souvent, les deux limites sont infinies.

Et bien sûr, l’image la plus évidente est l’hyperbole au point zéro. Ici, les deux limites unilatérales sont infinies : , la fonction subit donc une discontinuité du deuxième type au point .

J'essaie de remplir mes articles avec un contenu le plus diversifié possible, regardons donc le graphique d'une fonction qui n'a pas encore été rencontrée :

selon le schéma standard :

1) La fonction n'est pas définie à ce stade car le dénominateur tend vers zéro.

Bien sûr, on peut immédiatement conclure que la fonction subit une discontinuité au point , mais il serait bon de classifier la nature de la discontinuité, ce qui est souvent requis par la condition. Pour ça:

Permettez-moi de vous rappeler que par enregistrement, nous entendons nombre négatif infinitésimal, et sous l'entrée - nombre positif infinitésimal.

Les limites unilatérales sont infinies, ce qui signifie que la fonction subit une discontinuité de 2ème espèce au point . L'axe y est asymptote verticale pour le graphique.

Il n'est pas rare que les deux limites unilatérales existent, mais une seule d'entre elles est infinie, par exemple :

C'est le graphique de la fonction.

Nous examinons le point de continuité :

1) La fonction n'est pas définie à ce stade.

2) Calculons les limites unilatérales :

Nous parlerons de la méthode de calcul de ces limites unilatérales dans les deux derniers exemples de la conférence, bien que de nombreux lecteurs aient déjà tout vu et tout deviné.

La limite de gauche est finie et égale à zéro (on « ne va pas au point lui-même »), mais la limite de droite est infinie et la branche orange du graphe se rapproche de l'infini de son asymptote verticale, donné par l'équation (ligne pointillée noire).

La fonction en souffre donc discontinuité de deuxième type au point .

Comme pour une discontinuité de 1ère espèce, la fonction peut être définie au point de discontinuité lui-même. Par exemple, pour une fonction par morceaux N'hésitez pas à mettre un point noir gras à l'origine des coordonnées. A droite se trouve une branche d'une hyperbole et la limite de droite est infinie. Je pense que presque tout le monde a une idée de ce à quoi ressemble ce graphique.

Ce que tout le monde attendait avec impatience :

Comment examiner la continuité d’une fonction ?

L'étude d'une fonction de continuité en un point s'effectue selon un schéma de routine déjà établi, qui consiste à vérifier trois conditions de continuité :

Exemple 1

Fonction Explorer

Solution:

1) Le seul point dans le champ d'application est celui où la fonction n'est pas définie.

2) Calculons les limites unilatérales :

Les limites unilatérales sont finies et égales.

Ainsi, à ce moment-là, la fonction souffre d'une discontinuité amovible.

A quoi ressemble le graphique de cette fonction ?

je voudrais simplifier , et il semble qu'une parabole ordinaire soit obtenue. MAIS la fonction d'origine n'est pas définie au point , donc la clause suivante est requise :

Faisons le dessin :

Répondre: la fonction est continue sur toute la droite numérique sauf le point où elle subit une discontinuité amovible.

La fonction peut être définie plus en détail d'une manière bonne ou moins bonne, mais selon la condition, cela n'est pas requis.

Vous dites que c'est un exemple tiré par les cheveux ? Pas du tout. Cela s'est produit des dizaines de fois dans la pratique. La quasi-totalité des tâches du site proviennent de véritables travaux et tests indépendants.

Débarrassons-nous de nos modules préférés :

Exemple 2

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Exécutez le dessin.

Solution: Pour une raison quelconque, les étudiants ont peur et n'aiment pas les fonctions avec un module, même si elles n'ont rien de compliqué. Nous avons déjà abordé un peu ces choses dans la leçon. Transformations géométriques des graphiques. Le module étant non négatif, il est développé comme suit : , où « alpha » est une expression. Dans ce cas, notre fonction doit être écrite par morceaux :

Mais les fractions des deux morceaux doivent être réduites de . La réduction, comme dans l’exemple précédent, ne se fera pas sans conséquences. La fonction d'origine n'est pas définie au point puisque le dénominateur tend vers zéro. Par conséquent, le système doit en outre spécifier la condition et rendre la première inégalité stricte :

Parlons maintenant d'une technique de décision TRÈS UTILE: avant de finaliser la tâche sur un brouillon, il est avantageux de faire un dessin (peu importe si les conditions l'exigent ou non). Cela aidera, d'une part, à voir immédiatement les points de continuité et les points de discontinuité, et, d'autre part, cela vous protégera à 100 % des erreurs lors de la recherche de limites unilatérales.

Faisons le dessin. Conformément à nos calculs, à gauche du point il faut dessiner un fragment de parabole (couleur bleue), et à droite - un morceau de parabole (couleur rouge), alors que la fonction n'est pas définie au point lui-même :

En cas de doute, prenez quelques valeurs x et branchez-les dans la fonction (en vous rappelant que le module détruit l'éventuel signe moins) et vérifiez le graphique.

Examinons analytiquement la fonction de continuité :

1) La fonction n'est pas définie au point, on peut donc immédiatement dire qu'elle n'y est pas continue.

2) Établissons la nature de la discontinuité ; pour ce faire, nous calculons des limites unilatérales :

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point . Notez encore une fois que lors de la recherche de limites, peu importe que la fonction au point d'arrêt soit définie ou non.

Il ne reste plus qu'à transférer le dessin du brouillon (il a été réalisé comme avec l'aide de la recherche ;-)) et à terminer la tâche :

Répondre: la fonction est continue sur toute la droite numérique sauf au point où elle subit une discontinuité de première espèce avec un saut.

Parfois, ils nécessitent une indication supplémentaire du saut de discontinuité. Il est calculé simplement - de la limite droite, vous devez soustraire la limite gauche : , c'est-à-dire qu'au point d'arrêt, notre fonction a sauté de 2 unités (comme nous l'indique le signe moins).

Exemple 3

Fonction Explorer pour la continuité. Déterminer la nature des discontinuités de fonction, si elles existent. Faites un dessin.

Ceci est un exemple à résoudre par vous-même, un exemple de solution à la fin de la leçon.

Passons à la version la plus populaire et la plus répandue de la tâche, lorsque la fonction se compose de trois parties :

Exemple 4

Examiner la continuité d'une fonction et tracer un graphique de la fonction .

Solution: il est évident que les trois parties de la fonction sont continues sur les intervalles correspondants, il ne reste donc plus qu'à vérifier deux points de « jonction » entre les pièces. Commençons par faire un brouillon de dessin, j'ai commenté la technique de construction de manière suffisamment détaillée dans la première partie de l'article. La seule chose est qu'il faut suivre attentivement nos points singuliers : en raison de l'inégalité, la valeur appartient à la droite (point vert), et en raison de l'inégalité, la valeur appartient à la parabole (point rouge) :


Bon, en principe, tout est clair =) Il ne reste plus qu'à formaliser la décision. Pour chacun des deux points « de jonction », on vérifie classiquement 3 conditions de continuité :

JE) Nous examinons le point de continuité

1)

Les limites unilatérales sont finies et différentes, ce qui fait que la fonction subit une discontinuité de 1ère espèce avec un saut au point .

Calculons le saut de discontinuité comme la différence entre les limites droite et gauche :
, c'est-à-dire que le graphique a augmenté d'une unité.

II) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

– les limites unilatérales sont finies et égales, ce qui signifie qu’il existe une limite générale.

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Au stade final, nous transférons le dessin vers la version finale, après quoi nous mettons l'accord final :

Répondre: la fonction est continue sur toute la droite numérique, à l'exception du point où elle subit une discontinuité de première espèce avec un saut.

Exemple 5

Examiner une fonction pour la continuité et construire son graphique .

Ceci est un exemple de solution indépendante, une solution courte et un échantillon approximatif du problème à la fin de la leçon.

On peut avoir l’impression qu’à un moment donné la fonction doit être continue et à un autre il doit y avoir une discontinuité. En pratique, ce n’est pas toujours le cas. Essayez de ne pas négliger les exemples restants - il y aura plusieurs fonctionnalités intéressantes et importantes :

Exemple 6

Étant donné une fonction . Étudiez la fonction pour la continuité à certains points. Construisez un graphique.

Solution: et encore une fois, exécutez immédiatement le dessin sur le brouillon :

La particularité de ce graphique est que la fonction par morceaux est donnée par l'équation de l'axe des abscisses. Ici cette zone est dessinée en vert, mais dans un cahier elle est généralement soulignée en gras avec un simple crayon. Et bien sûr, n’oubliez pas nos béliers : la valeur appartient à la branche tangente (point rouge), et la valeur appartient à la droite.

Tout est clair sur le dessin - la fonction est continue sur toute la droite numérique, il ne reste plus qu'à formaliser la solution, qui est amenée à une automatisation complète littéralement après 3-4 exemples similaires :

JE) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Calculons les limites unilatérales :

, ce qui signifie qu'il existe une limite générale.

Au cas où, permettez-moi de vous rappeler un fait trivial : la limite d'une constante est égale à la constante elle-même. Dans ce cas, la limite de zéro est égale à zéro lui-même (limite à gauche).

3) – la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

II) Nous examinons le point de continuité

1) – la fonction est définie en un point donné.

2) Trouvez des limites unilatérales :

Et ici – la limite d’un est égale à l’unité elle-même.

– il existe une limite générale.

3) 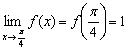– la limite d'une fonction en un point est égale à la valeur de cette fonction en un point donné.

Ainsi, une fonction est continue en un point par la définition de continuité d'une fonction en un point.

Comme d'habitude, après recherche nous transférons notre dessin vers la version finale.

Répondre: la fonction est continue aux points.

Veuillez noter que dans la condition on ne nous a rien demandé sur l'étude de la continuité de la fonction entière, et il est considéré comme une bonne forme mathématique de formuler précis et clair la réponse à la question posée. À propos, si les conditions ne vous obligent pas à construire un graphique, vous avez parfaitement le droit de ne pas le construire (bien que plus tard, l'enseignant puisse vous forcer à le faire).

Un petit « virelangue » mathématique pour le résoudre vous-même :

Exemple 7

Étant donné une fonction 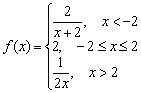. Étudiez la fonction pour la continuité à certains points. Classez les points d’arrêt, le cas échéant. Exécutez le dessin.

Essayez de "prononcer" tous les "mots" correctement =) Et dessinez le graphique plus précisément, avec précision, ce ne sera pas superflu partout ;-)

Comme vous vous en souvenez, j'ai recommandé de terminer immédiatement le dessin sous forme de brouillon, mais de temps en temps, vous rencontrez des exemples où vous ne pouvez pas comprendre immédiatement à quoi ressemble le graphique. Par conséquent, dans certains cas, il est avantageux de trouver d’abord les limites unilatérales et ensuite seulement, sur la base de l’étude, de représenter les branches. Dans les deux derniers exemples, nous apprendrons également une technique pour calculer certaines limites unilatérales :

Exemple 8

Examinez la continuité de la fonction et construisez son graphique schématique.

Solution: les mauvais points sont évidents : (réduit le dénominateur de l'exposant à zéro) et (réduit le dénominateur de la fraction entière à zéro). On ne sait pas exactement à quoi ressemble le graphique de cette fonction, ce qui signifie qu'il est préférable de faire d'abord quelques recherches.

Définition 4. Une fonction est dite continue sur un segment si elle est continue en tout point de ce segment (au point a elle est continue à droite, c'est-à-dire et au point b elle est continue à gauche, c'est-à-dire).

Toutes les fonctions élémentaires de base sont continues dans le domaine de leur définition.

Propriétés des fonctions continues sur un intervalle :

• 1) Si une fonction est continue sur un intervalle, alors elle est bornée sur cet intervalle (premier théorème de Weierstrass).
• 2) Si une fonction est continue sur un segment, alors sur ce segment elle atteint sa valeur minimale et sa valeur maximale (deuxième théorème de Weierstrass) (voir Fig. 2).
• 3) Si une fonction est continue sur un segment et prend des valeurs de signes différents à ses extrémités, alors à l'intérieur du segment il y a au moins un point tel que (théorème de Bolzano-Cauchy).

Points d'arrêt de fonction et leur classification

segment de point de continuité de fonction

Les points auxquels la condition de continuité n'est pas satisfaite sont appelés points d'arrêt de cette fonction. Si est un point de discontinuité d'une fonction, alors au moins une des trois conditions de continuité d'une fonction spécifiées dans les définitions 1, 2 n'est pas remplie, à savoir :

1) La fonction est définie au voisinage d'un point, mais pas définie au point lui-même. Ainsi la fonction considérée dans l'exemple 2 a) présente une discontinuité en un point, puisqu'elle n'est pas définie en ce point.

2) La fonction est définie en un point et ses environs, il y a des limites unilatérales et, mais elles ne sont pas égales entre elles : . Par exemple, la fonction de l'exemple 2 b) est définie en un point et son voisinage, mais, puisque a.

3) La fonction est définie au point et à ses environs, il y a des limites unilatérales et elles sont égales entre elles, mais pas égales à la valeur de la fonction au point : . Par exemple, une fonction. Voici le point de rupture : à ce stade la fonction est définie, il y a des limites unilatérales et égales les unes aux autres, mais, c'est-à-dire .

Les points d’arrêt des fonctions sont classés comme suit.

Définition 5. Un point est appelé point de discontinuité du premier type de fonction si en ce point il existe des limites finies et, mais elles ne sont pas égales entre elles : . La quantité est appelée le saut de la fonction en un point.

Définition 6. Un point est appelé point de discontinuité amovible d'une fonction si en ce point il y a des limites finies et, elles sont égales les unes aux autres : , mais la fonction elle-même n'est pas définie au point, ou est définie, mais.

Définition 7. Un point est appelé point de discontinuité du deuxième type de fonction si à ce point au moins une des limites unilatérales (ou) n'existe pas ou est égale à l'infini.

Exemple 3. Trouvez les points d'arrêt des fonctions suivantes et déterminez leur type : a) b)

Solution. a) La fonction est définie et continue sur des intervalles, et, puisque sur chacun de ces intervalles elle est définie par des fonctions élémentaires continues. Par conséquent, les points d'arrêt d'une fonction donnée ne peuvent être que les points auxquels la fonction change de tâche analytique, c'est-à-dire points et Trouvons les limites unilatérales de la fonction au point :

Puisque les limites unilatérales existent et sont finies, mais ne sont pas égales les unes aux autres, le point est un point de discontinuité du premier type. Saut de fonction :

Pour le point que nous trouvons.

Une fonction est dite continue en un point x0 si f(x) tend vers f(x0) comme x tend vers x0. Dans ce cas, f(x) - A = f(x) - f(x0) = ∆f. Si une fonction f est continue en tout point d'un certain intervalle A, alors cette fonction sera continue sur tout l'intervalle A. Et l'intervalle A lui-même est appelé dans ce cas écart de continuité fonctions f.

Le graphique des fonctions continues étudiées dans un cours de mathématiques à l'école peut être tracé « sans retirer le crayon du papier », puisqu'il s'agit d'une ligne continue. Si sur un intervalle (a;b) la fonction f est continue et ne disparaît pas, alors sur cet intervalle elle conservera un signe constant.

Cette propriété est très facile à comprendre. La fonction située au dessus de l'axe Ox a un signe plus, la fonction située en dessous de l'axe Ox a un signe moins. Si la ligne de fonction ne coupe pas l'axe Ox (la fonction est nulle sur l'axe Ox), alors elle ne changera clairement pas de signe.

Méthode d'intervalle

Une application frappante des propriétés de continuité des fonctions est la méthode des intervalles, qui est utilisée pour résoudre les inégalités dans une variable. Supposons qu'une fonction soit continue sur l'intervalle A et disparaisse en un nombre fini de points appartenant à cet intervalle.

En utilisant la propriété donnée ci-dessus, ces points diviseront tout l'intervalle A en intervalles dans lesquels la fonction conservera son signe. Pour déterminer les signes de tous les intervalles, il suffit de connaître le signe de l'un quelconque de ces intervalles.

Exemple de fonction qui n'est pas continue

Jusqu’à présent, nous n’avons rencontré que des fonctions continues. Mais il existe des fonctions qui ne sont pas continues à chaque point où elles sont définies. Par exemple, la fonction f(x) = (x), où (x) est la partie fractionnaire du nombre x. Son graphique est présenté dans la figure suivante.

Il est facile de voir que la propriété principale de continuité d’une fonction au point x0 égale à tout nombre entier ne sera pas satisfaite. Mais en même temps, la fonction f(x) = (x) est continue en tous les autres points auxquels elle est définie, à l'exception des points où x est égal à un nombre entier. Sur le graphique, ces points sont marqués de cercles perforés.

Fonctions continues mais non différentiables en un point donné

Il existe des fonctions qui sont continues en tout point de leur domaine de définition. Mais en même temps, ils n’auront pas de produits dérivés à certains moments. Par exemple, la fonction y=|x| est continue sur toute la ligne numérique, mais n'est pas dérivable au point x = 0. Vous trouverez ci-dessous un graphique de cette fonction.

Dans cette leçon, nous apprendrons comment établir la continuité d'une fonction. Nous le ferons en utilisant des limites, unilatérales en plus - droite et gauche, qui ne font pas du tout peur, malgré le fait qu'elles s'écrivent comme et .

Mais qu’est-ce que la continuité d’une fonction ? En attendant d'arriver à une définition stricte, il est plus facile d'imaginer une ligne qui peut être tracée sans retirer le crayon du papier. Si une telle ligne est tracée, alors elle est continue. Cette droite est le graphique d’une fonction continue.

Graphiquement, une fonction est continue en un point si son graphique ne se « casse » pas en ce point. Le graphique d’une telle fonction continue est illustré dans la figure ci-dessous.

Détermination de la continuité d'une fonction à travers une limite. Une fonction est continue en un point si trois conditions sont remplies :

1. La fonction est définie au point .

Si au moins une des conditions énumérées n’est pas remplie, la fonction n’est pas continue à ce stade. Dans ce cas, ils disent que la fonction souffre d'une discontinuité, et les points du graphique où le graphique est interrompu sont appelés points de discontinuité de la fonction. Le graphique d'une telle fonction qui subit une discontinuité au point x=2 est dans la figure ci-dessous.

Exemple 1. Fonction F(X) est défini comme suit :

Cette fonction sera-t-elle continue à chacun des points limites de ses branches, c'est-à-dire aux points X = 0 , X = 1 , X = 3 ?

Solution. Nous vérifions les trois conditions pour la continuité d'une fonction à chaque point frontière. La première condition est remplie, puisque quoi fonction définieà chacun des points limites découle de la définition de la fonction. Reste à vérifier les deux conditions restantes.

Point X= 0 . Trouvons la limite de gauche à ce stade :

.

Trouvons la limite de droite :

X= 0 doit être trouvé pour la branche de la fonction qui inclut ce point, c'est-à-dire la deuxième branche. On les retrouve :

Comme on peut le voir, la limite de la fonction et la valeur de la fonction au point X= 0 sont égaux. La fonction est donc continue au point X = 0 .

Point X= 1 . Trouvons la limite de gauche à ce stade :

Trouvons la limite de droite :

Limite d'une fonction et valeur d'une fonction en un point X= 1 doit être trouvé pour la branche de la fonction qui inclut ce point, c'est-à-dire la deuxième branche. On les retrouve :

.

Limite d'une fonction et valeur d'une fonction en un point X= 1 sont égaux. La fonction est donc continue au point X = 1 .

Point X= 3 . Trouvons la limite de gauche à ce stade :

Trouvons la limite de droite :

Limite d'une fonction et valeur d'une fonction en un point X= 3 doit être trouvé pour la branche de la fonction qui inclut ce point, c'est-à-dire la deuxième branche. On les retrouve :

.

Limite d'une fonction et valeur d'une fonction en un point X= 3 sont égaux. La fonction est donc continue au point X = 3 .

La conclusion principale : cette fonction est continue en chaque point frontière.

Établissez vous-même la continuité d'une fonction en un point, puis regardez la solution

Un changement continu dans une fonction peut être défini comme un changement progressif, sans sauts, dans lequel un petit changement dans l'argument entraîne un petit changement dans la fonction.

Illustrons ce changement continu de fonction par un exemple.

Laissez un poids pendre à un fil au-dessus de la table. Sous l'influence de cette charge, le fil s'étire, donc la distance je la charge à partir du point de suspension du fil est fonction de la masse de la charge m, c'est je = F(m) , m≥0 .

Si vous modifiez légèrement la masse de la charge, alors la distance je changera peu : petits changements m de petits changements correspondent je. Cependant, si la masse de la charge est proche de la résistance à la traction du filetage, alors une légère augmentation de la masse de la charge peut provoquer la rupture du filetage : distance je augmentera brusquement et deviendra égale à la distance entre le point de suspension et la surface de la table. Graphique d'une fonction je = F(m) montré sur la figure. Au niveau d'une section, ce graphique est une ligne continue (solide) et à un moment donné, il est interrompu. Le résultat est un graphe composé de deux branches. En tous points sauf , la fonction je = F(m) est continu, mais en un point il présente une discontinuité.

L'étude de la continuité d'une fonction peut être soit une tâche indépendante, soit l'une des étapes d'une étude complète de la fonction et de la construction de son graphique.

Continuité d'une fonction sur un intervalle

Laissez la fonction oui = F(X) défini dans l'intervalle ] un, b[ et est continue en tout point de cet intervalle. Alors on l'appelle continu dans l'intervalle ] un, b[ . La notion de continuité d'une fonction sur des intervalles de la forme ]- ∞ se définit de la même manière, b[ , ]un, + ∞[ , ]- ∞, + ∞[ . Laissez maintenant la fonction oui = F(X) défini sur l'intervalle [ un, b] . La différence entre un intervalle et un segment : les points limites d'un intervalle ne sont pas inclus dans l'intervalle, mais les points limites d'un segment sont inclus dans le segment. Il convient ici de mentionner ce qu'on appelle la continuité unilatérale : au point un, restant sur le segment [ un, b] , on ne peut approcher que par la droite, et au point b- seulement à gauche. La fonction est dite continue sur l’intervalle [ un, b] , s'il est continu en tous les points intérieurs de ce segment, continu à droite au point un et reste continu au point b.

Un exemple de fonction continue peut être n'importe laquelle des fonctions élémentaires. Chaque fonction élémentaire est continue sur tout intervalle sur lequel elle est définie. Par exemple, les fonctions et sont continues sur n'importe quel intervalle [ un, b], la fonction est continue sur l'intervalle [ 0 , b] , la fonction est continue sur tout segment ne contenant pas de point un = 2 .

Exemple 4. Examinez la fonction pour la continuité.

Solution. Vérifions la première condition. La fonction n'est pas définie aux points - 3 et 3. Au moins une des conditions de continuité de la fonction sur toute la droite numérique n'est pas remplie. Cette fonction est donc continue sur les intervalles

Exemple 5. Déterminer à quelle valeur du paramètre un continu tout au long domaine de définition fonction

Solution.

Trouvons la limite de droite à :

.

Évidemment, la valeur au point X= 2 devrait être égal hache :

un = 1,5 .

Exemple 6. Déterminer à quelles valeurs de paramètre un Et b continu tout au long domaine de définition fonction

Solution.
Trouvons la limite gauche de la fonction au point :

.

Par conséquent, la valeur au point doit être 1 :

Trouvons la fonction de gauche au point :

Évidemment, la valeur de la fonction en un point doit être égale à :

Réponse : la fonction est continue sur tout le domaine de définition lorsque un = 1; b = -3 .

Propriétés de base des fonctions continues

Les mathématiques sont parvenues au concept de fonction continue en étudiant tout d’abord diverses lois du mouvement. L'espace et le temps sont infinis, et la dépendance, par exemple, des chemins s de temps t, exprimé par la loi s = F(t) , donne un exemple d'un continu les fonctions F(t) . La température de l’eau chauffée change également de façon continue ; c’est aussi une fonction continue du temps : T = F(t) .

En analyse mathématique, certaines propriétés des fonctions continues sont prouvées. Présentons la plus importante de ces propriétés.

1. Si une fonction continue sur un intervalle prend des valeurs de signes différents aux extrémités de l'intervalle, alors à un moment donné de cet intervalle, elle prend une valeur égale à zéro. De manière plus formelle, cette propriété est donnée dans un théorème connu sous le nom de premier théorème de Bolzano-Cauchy.

2. Fonction F(X) , continue sur l'intervalle [ un, b] , prend toutes les valeurs intermédiaires entre les valeurs aux points finaux, c'est-à-dire entre F(un) Et F(b) . Dans une formulation plus formelle, cette propriété est donnée dans un théorème connu sous le nom de deuxième théorème de Bolzano-Cauchy.