Combien y a-t-il d’angles égaux dans un parallélogramme ? Propriété des diagonales d'un parallélogramme

1. Définition d'un parallélogramme.

Si nous croisons une paire de droites parallèles avec une autre paire de droites parallèles, nous obtenons un quadrilatère dont les côtés opposés sont parallèles deux à deux.

Dans les quadrilatères ABDC et EFNM (Fig. 224) ВD || AC et AB || CD;

FE || MN et EM || FN.

Un quadrilatère dont les côtés opposés sont parallèles deux à deux s’appelle un parallélogramme.

2. Propriétés d'un parallélogramme.

Théorème. La diagonale d'un parallélogramme le divise en deux triangles égaux.

Soit un parallélogramme ABDC (Fig. 225), dans lequel AB || CD et CA || ВD.

Vous devez prouver que la diagonale le divise en deux triangles égaux.

Traçons la diagonale CB dans le parallélogramme ABDC. Montrons que $\Delta$CAB = $\Delta$СДВ.

Le côté NE est commun à ces triangles ; ∠ABC = ∠BCD, comme angles transversaux internes avec AB et CD parallèles et CB sécants ; ∠ACB = ∠СВD, ainsi que les angles transversaux internes avec AC et BD parallèles et CB sécants.

D'où $\Delta$CAB = $\Delta$СДВ.

De la même manière, on peut prouver que la diagonale AD divisera le parallélogramme en deux triangles égaux ACD et ABD.

Conséquences:

1 . Les angles opposés d'un parallélogramme sont égaux.

∠A = ∠D, cela découle de l'égalité des triangles CAB et CDB.

De même, ∠C = ∠B.

2. Les côtés opposés d’un parallélogramme sont égaux.

AB = CD et AC = BD, puisque ce sont des côtés de triangles égaux et des angles opposés égaux.

Théorème 2. Les diagonales d'un parallélogramme sont divisées en deux au point de leur intersection.

Soient BC et AD les diagonales du parallélogramme ABC (Fig. 226). Montrons que AO = OD et CO = OB.

Pour ce faire, comparez une paire de triangles situés de manière opposée, par exemple $\Delta$AOB et $\Delta$COD.

Dans ces triangles AB = CD, comme les côtés opposés d'un parallélogramme ;

∠1 = ∠2, comme angles internes croisés avec les parallèles AB et CD et sécants AD ;

∠3 = ∠4 pour la même raison, puisque AB || CD et SV sont leurs sécantes.

Il s’ensuit que $\Delta$AOB = $\Delta$СOD. Et dans les triangles égaux, les côtés égaux se trouvent en face des angles égaux. Par conséquent, AO = OD et CO = OB.

Théorème 3. La somme des angles adjacents à un côté d'un parallélogramme est égale à 180°.

Dans le parallélogramme ABCD, nous traçons la diagonale AC et obtenons deux triangles ABC et ADC.

Les triangles sont égaux, puisque ∠1 = ∠4, ∠2 = ∠3 (angles transversaux pour les lignes parallèles) et le côté AC est commun.
De l'égalité $\Delta$ABC = $\Delta$ADC il s'ensuit que AB = CD, BC = AD, ∠B = ∠D.

La somme des angles adjacents à un côté, par exemple les angles A et D, est égale à 180° comme angles unilatéraux pour les droites parallèles.

Notes IMPORTANTES!
1. Si vous voyez du charabia au lieu de formules, videz votre cache. Comment faire cela dans votre navigateur est écrit ici :
2. Avant de commencer à lire l'article, faites attention à notre navigateur pour connaître les ressources les plus utiles pour

1. Parallélogramme

Mot composé « parallélogramme » ? Et derrière cela se cache une figure très simple.

Eh bien, nous avons pris deux lignes parallèles :

Traversé par deux autres :

Et à l'intérieur il y a un parallélogramme !

Quelles propriétés possède un parallélogramme ?

Propriétés d'un parallélogramme.

Autrement dit, que pouvez-vous utiliser si le problème est un parallélogramme ?

Le théorème suivant répond à cette question :

Dessinons tout en détail.

Qu'est-ce que ça veut dire premier point du théorème? Et le fait est que si vous AVEZ un parallélogramme, alors vous le ferez certainement

Le deuxième point signifie que s’il existe un parallélogramme, alors, encore une fois, certainement :

Eh bien, et enfin, le troisième point signifie que si vous AVEZ un parallélogramme, alors assurez-vous de :

Voyez-vous quelle richesse de choix il y a ? Que faut-il utiliser dans le problème ? Essayez de vous concentrer sur la question de la tâche, ou essayez simplement tout un par un - une « clé » fera l'affaire.

Posons-nous maintenant une autre question : comment reconnaître un parallélogramme « à vue » ? Que doit-il arriver à un quadrilatère pour qu’on ait le droit de lui donner le « titre » de parallélogramme ?

Plusieurs signes d'un parallélogramme répondent à cette question.

Signes d'un parallélogramme.

Attention! Commencer.

Parallélogramme.

Attention : si vous avez trouvé au moins un signe dans votre problème, alors vous avez définitivement un parallélogramme et vous pouvez utiliser toutes les propriétés d'un parallélogramme.

2. Rectangulaire

Je pense que ce ne sera pas du tout nouveau pour toi

Première question : un rectangle est-il un parallélogramme ?

Bien sûr que oui ! Après tout, il a - vous vous souvenez, notre signe 3 ?

Et de là, bien sûr, il s'ensuit que dans un rectangle, comme dans tout parallélogramme, les diagonales sont divisées en deux par le point d'intersection.

Mais le rectangle a aussi une propriété distinctive.

Propriété rectangulaire

Pourquoi cette propriété est-elle distinctive ? Parce qu’aucun autre parallélogramme n’a des diagonales égales. Formulons-le plus clairement.

Attention : pour devenir un rectangle, le quadrilatère doit d'abord devenir un parallélogramme, puis montrer l'égalité des diagonales.

3. Diamant

Et encore la question : un losange est-il un parallélogramme ou pas ?

De plein droit - un parallélogramme, car il a et (rappelez-vous notre fonctionnalité 2).

Et encore une fois, puisqu'un losange est un parallélogramme, alors il doit avoir toutes les propriétés d'un parallélogramme. Cela signifie que dans un losange, les angles opposés sont égaux, les côtés opposés sont parallèles et les diagonales se coupent en deux au point d'intersection.

Propriétés d'un losange

Regarde l'image:

Comme dans le cas d'un rectangle, ces propriétés sont distinctives, c'est-à-dire que pour chacune de ces propriétés, nous pouvons conclure qu'il ne s'agit pas simplement d'un parallélogramme, mais d'un losange.

Signes d'un diamant

Et encore une fois, faites attention : il ne doit pas y avoir seulement un quadrilatère dont les diagonales sont perpendiculaires, mais un parallélogramme. S'assurer:

Non, bien sûr, bien que ses diagonales soient perpendiculaires et que la diagonale soit la bissectrice des angles et. Mais... les diagonales ne sont pas divisées en deux par le point d'intersection, donc - PAS un parallélogramme, et donc PAS un losange.

Autrement dit, un carré est à la fois un rectangle et un losange. Voyons ce qui se passe.

Est-ce clair pourquoi ? - le losange est la bissectrice de l'angle A, qui est égale à. Cela signifie qu'il se divise (et aussi) en deux angles.

Eh bien, c'est très clair : les diagonales d'un rectangle sont égales ; Les diagonales d'un losange sont perpendiculaires, et en général, un parallélogramme de diagonales est divisé en deux par le point d'intersection.

NIVEAU MOYEN

Propriétés des quadrilatères. Parallélogramme

Propriétés d'un parallélogramme

Attention! Mots " propriétés d'un parallélogramme"ça veut dire que si dans ta tâche Il y a parallélogramme, alors tous les éléments suivants peuvent être utilisés.

Théorème sur les propriétés d'un parallélogramme.

Dans n'importe quel parallélogramme :

Comprenons pourquoi tout cela est vrai, en d'autres termes NOUS PROUVONS théorème.

Alors pourquoi 1) est-il vrai ?

Si c'est un parallélogramme, alors :

mentir comme entrecroisé
couchés comme des croix.

Cela signifie (selon le critère II : et - général.)

Eh bien, c'est ça, c'est ça ! - prouvé.

Mais au fait ! Nous avons également prouvé 2) !

Pourquoi? Mais (regardez la photo), c'est précisément parce que.

Il en reste 3).

Pour ce faire, il faut encore tracer une deuxième diagonale.

Et maintenant nous voyons cela - selon la caractéristique II (les angles et le côté « entre » eux).

Propriétés prouvées ! Passons aux signes.

Signes d'un parallélogramme

Rappelons que le signe du parallélogramme répond à la question « comment savez-vous qu'une figure est un parallélogramme ?

En icônes, c'est comme ça :

Pourquoi? Ce serait bien de comprendre pourquoi - ça suffit. Mais regarde:

Eh bien, nous avons compris pourquoi le signe 1 est vrai.

Eh bien, c'est encore plus simple ! Traçons à nouveau une diagonale.

Ce qui signifie:

ET C'est aussi facile. Mais différent!

Moyens, . Ouah! Mais aussi - interne unilatéral avec une sécante !

Donc le fait que cela signifie cela.

Et si vous regardez de l'autre côté, alors - interne unilatéral avec une sécante ! Et donc.

Voyez-vous à quel point c'est génial ?!

Et encore une fois simple :

Exactement pareil, et.

Faites attention: si tu as trouvé au moins un signe de parallélogramme dans votre problème, alors vous avez exactement parallélogramme et vous pouvez utiliser tout le monde propriétés d'un parallélogramme.

Pour plus de clarté, regardez le schéma :

Propriétés des quadrilatères. Rectangle.

Propriétés du rectangle :

Le point 1) est assez évident - après tout, le signe 3 () est simplement rempli

Et point 2) - très important. Alors prouvons que

Cela signifie des deux côtés (et - en général).

Eh bien, puisque les triangles sont égaux, alors leurs hypoténuses sont également égales.

Prouvé cela!

Et imaginez, l'égalité des diagonales est une propriété distinctive d'un rectangle parmi tous les parallélogrammes. Autrement dit, cette affirmation est vraie^

Comprenons pourquoi ?

Cela signifie (c'est-à-dire les angles d'un parallélogramme). Mais rappelons encore une fois qu'il s'agit d'un parallélogramme, et donc.

Moyens, . Eh bien, bien sûr, il s'ensuit que chacun d'eux ! Après tout, ils doivent tout donner !

Ils ont donc prouvé que si parallélogramme du coup (!) les diagonales s'avèrent égales, alors ça exactement un rectangle.

Mais! Faites attention! C'est à propos de parallélogrammes! Pas n'importe qui un quadrilatère avec des diagonales égales est un rectangle, et seulement parallélogramme!

Propriétés des quadrilatères. Rhombe

Et encore la question : un losange est-il un parallélogramme ou pas ?

De plein droit - un parallélogramme, car il en a (rappelez-vous notre fonctionnalité 2).

Et encore une fois, puisqu’un losange est un parallélogramme, il doit avoir toutes les propriétés d’un parallélogramme. Cela signifie que dans un losange, les angles opposés sont égaux, les côtés opposés sont parallèles et les diagonales se coupent en deux au point d'intersection.

Mais il existe aussi des propriétés particulières. Formulons-le.

Propriétés d'un losange

Pourquoi? Eh bien, puisqu'un losange est un parallélogramme, alors ses diagonales sont divisées en deux.

Pourquoi? Oui, c'est pourquoi !

En d’autres termes, les diagonales se sont révélées être les bissectrices des coins du losange.

Comme dans le cas d'un rectangle, ces propriétés sont distinctif, chacun d'eux est aussi le signe d'un losange.

Signes d'un diamant.

Pourquoi est-ce? Et regarde,

Cela signifie les deux Ces triangles sont isocèles.

Pour être un losange, un quadrilatère doit d’abord « devenir » un parallélogramme, puis présenter la caractéristique 1 ou la caractéristique 2.

Propriétés des quadrilatères. Carré

Autrement dit, un carré est à la fois un rectangle et un losange. Voyons ce qui se passe.

Est-ce clair pourquoi ? Un carré - un losange - est la bissectrice d'un angle égal à. Cela signifie qu'il se divise (et aussi) en deux angles.

Pourquoi? Eh bien, appliquons simplement le théorème de Pythagore à...

RÉSUMÉ ET FORMULES DE BASE

Propriétés d'un parallélogramme :

Les côtés opposés sont égaux : , .
Les angles opposés sont égaux : , .
Les angles d'un côté totalisent : , .
Les diagonales sont divisées en deux par le point d'intersection : .

Propriétés du rectangle :

Les diagonales du rectangle sont égales : .
Un rectangle est un parallélogramme (pour un rectangle toutes les propriétés d'un parallélogramme sont remplies).

Propriétés d'un losange :

Les diagonales d'un losange sont perpendiculaires : .
Les diagonales d'un losange sont les bissectrices de ses angles : ; ; ; .
Un losange est un parallélogramme (pour un losange toutes les propriétés d'un parallélogramme sont remplies).

Propriétés d'un carré :

Un carré est à la fois un losange et un rectangle, donc pour un carré toutes les propriétés d'un rectangle et d'un losange sont remplies. Et:

Eh bien, le sujet est terminé. Si vous lisez ces lignes, c’est que vous êtes très cool.

Parce que seulement 5 % des gens sont capables de maîtriser quelque chose par eux-mêmes. Et si vous lisez jusqu'au bout, alors vous êtes dans ces 5% !

Maintenant, le plus important.

Vous avez compris la théorie sur ce sujet. Et je le répète, ça... c'est juste super ! Vous êtes déjà meilleur que la grande majorité de vos pairs.

Le problème est que cela ne suffit peut-être pas...

Pour quoi?

Pour avoir réussi l'examen d'État unifié, pour entrer à l'université avec un budget limité et, SURTOUT, pour la vie.

Je ne vais vous convaincre de rien, je dirai juste une chose...

Les personnes qui ont reçu une bonne éducation gagnent beaucoup plus que celles qui ne l’ont pas reçue. Ce sont des statistiques.

Mais ce n’est pas l’essentiel.

L'essentiel est qu'ils soient PLUS HEUREUX (il existe de telles études). Peut-être parce que de nombreuses autres opportunités s'ouvrent devant eux et que la vie devient plus lumineuse ? Je ne sais pas...

Mais pensez par vous-même...

Que faut-il pour être sûr d'être meilleur que les autres à l'examen d'État unifié et finalement être... plus heureux ?

GAGNEZ VOTRE MAIN EN RÉSOUDANT DES PROBLÈMES SUR CE SUJET.

Aucune théorie ne vous sera demandée pendant l'examen.

Tu auras besoin de résoudre des problèmes contre le temps.

Et si vous ne les avez pas résolus (BEAUCOUP !), vous ferez certainement une erreur stupide quelque part ou vous n’aurez tout simplement pas le temps.

C'est comme dans le sport : il faut répéter plusieurs fois pour gagner avec certitude.

Retrouvez la collection où vous voulez, nécessairement avec des solutions, une analyse détaillée et décidez, décidez, décidez !

Vous pouvez utiliser nos tâches (facultatif) et nous les recommandons bien sûr.

Afin de mieux utiliser nos tâches, vous devez contribuer à prolonger la durée de vie du manuel YouClever que vous lisez actuellement.

Comment? Il existe deux options :

Débloquez toutes les tâches cachées dans cet article -
Débloquez l'accès à toutes les tâches cachées dans les 99 articles du manuel - Acheter un manuel - 499 RUR

Oui, nous avons 99 articles de ce type dans notre manuel et l'accès à toutes les tâches et à tous les textes cachés qu'elles contiennent peut être ouvert immédiatement.

L'accès à toutes les tâches cachées est assuré pendant TOUTE la vie du site.

En conclusion...

Si vous n'aimez pas nos tâches, trouvez-en d'autres. Ne vous arrêtez pas à la théorie.

« Compris » et « Je peux résoudre » sont des compétences complètement différentes. Vous avez besoin des deux.

Trouvez les problèmes et résolvez-les !

Établissement d'enseignement budgétaire municipal

Lycée Savinskaïa

Recherche

Parallélogramme et ses nouvelles propriétés

Complété par : élève de 8B

École secondaire MBOU Savinskaya

Kuznetsova Svetlana, 14 ans

Responsable : professeur de mathématiques

Toultchevskaya N.A.

Région d'Ivanovo, Russie

2016

JE. Introduction ___________________________________________________page 3

II. De l'histoire du parallélogramme ___________________________________page 4

III Propriétés supplémentaires d'un parallélogramme ____________________________________________page 4

IV. Preuve de propriété _____________________________________ page 5

V. Résolution de problèmes à l'aide de propriétés supplémentaires __________page 8

VI. Application des propriétés d'un parallélogramme dans la vie ___________________page 11

VII. Conclusion _________________________________________________page 12

VIII. Littérature _________________________________________________page 13

Introduction

"Entre esprits égaux

à égalité des autres conditions

celui qui connaît la géométrie est supérieur"

(Blaise Pascal).

En étudiant le sujet « Parallélogramme » dans les cours de géométrie, nous avons examiné deux propriétés d'un parallélogramme et trois caractéristiques, mais lorsque nous avons commencé à résoudre des problèmes, il s'est avéré que cela ne suffisait pas.

J'avais une question : un parallélogramme a-t-il d'autres propriétés et comment aideront-elles à résoudre des problèmes ?

Et j'ai décidé d'étudier des propriétés supplémentaires d'un parallélogramme et de montrer comment elles peuvent être appliquées pour résoudre des problèmes.

Sujet d'étude : parallélogramme

Objet d'étude : propriétés d'un parallélogramme
Objectif du travail :

formulation et preuve de propriétés supplémentaires d'un parallélogramme qui ne sont pas étudiées à l'école ;

application de ces propriétés pour résoudre des problèmes.

Tâches:

Étudier l'histoire de l'apparition du parallélogramme et l'histoire du développement de ses propriétés ;

Trouver de la littérature supplémentaire sur la question à l'étude ;

Étudier les propriétés supplémentaires d'un parallélogramme et les prouver ;

Montrer l'application de ces propriétés pour résoudre des problèmes ;

Considérez l'application des propriétés d'un parallélogramme dans la vie.
Méthodes de recherche:

Travailler avec de la littérature pédagogique et scientifique populaire, des ressources Internet ;

Étude du matériel théorique ;

Identification d'une gamme de problèmes qui peuvent être résolus en utilisant les propriétés supplémentaires d'un parallélogramme ;

Observation, comparaison, analyse, analogie.

Durée de l'étude : 3 mois : janvier-mars 2016

Dans un manuel de géométrie, nous lisons la définition suivante d'un parallélogramme : Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles deux à deux.

Le mot « parallélogramme » est traduit par « lignes parallèles » (des mots grecs Parallélos - parallèle et gramme - ligne), ce terme a été introduit par Euclide. Dans son livre Éléments, Euclide a prouvé les propriétés suivantes d'un parallélogramme : les côtés et les angles opposés d'un parallélogramme sont égaux et la diagonale le coupe en deux. Euclide ne mentionne pas le point d'intersection d'un parallélogramme. Ce n’est que vers la fin du Moyen Âge qu’une théorie complète des parallélogrammes a été développée et ce n’est qu’au XVIIe siècle que des théorèmes sur les parallélogrammes sont apparus dans les manuels, qui sont prouvés à l’aide du théorème d’Euclide sur les propriétés d’un parallélogramme.

III Propriétés supplémentaires d'un parallélogramme

Dans le manuel de géométrie, seules 2 propriétés d'un parallélogramme sont données :

Les angles et côtés opposés sont égaux

Les diagonales d'un parallélogramme se coupent et sont divisées en deux par le point d'intersection.

Dans diverses sources sur la géométrie, vous pouvez trouver les propriétés supplémentaires suivantes :

La somme des angles adjacents d'un parallélogramme est 180 0

La bissectrice de l'angle d'un parallélogramme en coupe un triangle isocèle ;

Les bissectrices des angles opposés d'un parallélogramme se trouvent sur des lignes parallèles ;

Les bissectrices des angles adjacents d'un parallélogramme se coupent à angle droit ;

Lorsque les bissectrices de tous les angles d'un parallélogramme se coupent, elles forment un rectangle ;

Les distances entre les coins opposés d'un parallélogramme et la même diagonale sont égales.

Si vous connectez des sommets opposés dans un parallélogramme avec les milieux des côtés opposés, vous obtenez un autre parallélogramme.

La somme des carrés des diagonales d'un parallélogramme est égale au double de la somme des carrés de ses côtés adjacents.

Si vous dessinez des altitudes sous deux angles opposés dans un parallélogramme, vous obtenez un rectangle.

IV Preuve des propriétés d'un parallélogramme

La somme des angles adjacents d'un parallélogramme est 180 0

Donné:

ABCD – parallélogramme

Prouver:

A+
B=

Preuve:

Un et
B – angles internes unilatéraux avec lignes droites parallèles BC AD et sécante AB, ce qui signifie
A+
B=

Donné: A B C D - parallélogramme,

Bissectrice AK
UN.

Prouver: AVK – isocèle

Preuve:

1)
1=
3 (en travers en position BC AD et sécante AK ),

2)
2=
3 car AK est une bissectrice,

signifie 1=
2.

3) ABC - isocèle car 2 angles d'un triangle sont égaux

. La bissectrice de l'angle d'un parallélogramme en coupe un triangle isocèle

Donné: ABCD est un parallélogramme,

AK – bissectrice A,

CP - bissectrice C.

Prouver: AK ║ SR

Preuve:

1) 1=2 car AK est une bissectrice

2) 4=5 parce que CP – bissectrice

3) 3=1 (angles transversaux à

BC ║ AD et AK-sécante),

4) A =C (par la propriété d'un parallélogramme), ce qui signifie 2=3=4=5.

4) Des paragraphes 3 et 4 il résulte que 1 = 4, et ces angles correspondent aux droites AK et CP et sécantes BC,

cela signifie AK ║ CP (basé sur le parallélisme des droites)

. Les bissectrices des angles opposés d'un parallélogramme se trouvent sur des lignes parallèles

Les bissectrices des angles adjacents d'un parallélogramme se coupent à angle droit

Donné: ABCD - parallélogramme,

AK-bissectrice A,

DP bissectrice D

Prouver: DP AK.

Preuve:

1) 1=2, parce que AK - bissectrice

Soit 1=2=x, alors A=2x,

2) 3=4, parce que D Р – bissectrice

Soit 3=4=y, alors D=2y

3) A + D =180 0, car la somme des angles adjacents d'un parallélogramme est 180

2) Considérez Une DO

1+3=90 0 , alors
<5=90 0 (сумма углов треугольников равна 180 0)

5. Les bissectrices de tous les angles d'un parallélogramme lors de leur intersection forment un rectangle

Donné: ABCD - parallélogramme, AK-bissectrice A,

DP-bissectrice D,

CM bissectrice C,

BF - bissectrice B .

Prouver: KRNS - rectangle

Preuve:

Basé sur la propriété précédente 8=7=6=5=90 0 ,

signifie que KRNS est un rectangle.

Les distances entre les coins opposés d'un parallélogramme et la même diagonale sont égales.

Donné: Parallélogramme ABCD, diagonale AC.

Capital-risque ca, D.P. A.C.

Prouver: BC = DP

Preuve: 1) DCP = KAB, comme croisements internes couchés avec AB ║ CD et AC sécants.

2) AKB= CDP (le long du côté et de deux angles adjacents AB=CD CD P=AB K).

Et dans des triangles égaux, les côtés correspondants sont égaux, ce qui signifie DP=BK.

Si vous connectez des sommets opposés dans un parallélogramme avec les milieux des côtés opposés, vous obtenez un autre parallélogramme.

Donné: Parallélogramme ABCD.

Prouver: VKDP est un parallélogramme.

Preuve:

1) BP=KD (AD=BC, points K et P

divisez ces côtés en deux)

2) BP ║ KD (mentir sur AD AVANT JC)

Si les côtés opposés d’un quadrilatère sont égaux et parallèles, alors le quadrilatère est un parallélogramme.

Si vous dessinez des altitudes sous deux angles opposés dans un parallélogramme, vous obtenez un rectangle.

La somme des carrés des diagonales d'un parallélogramme est égale au double de la somme des carrés de ses côtés adjacents.

Donné: ABCD est un parallélogramme. BD et AC sont des diagonales.

Prouver: CA 2 +ВD 2 =2(AB 2 + annonce 2 )

Preuve: 1)DEMANDER: A.C. ²=
+

2)B R.D : BD 2 = B R. 2 +RD 2 (d'après le théorème de Pythagore)

3) A.C. ²+ BD ²=SK²+UN K²+B Р²+РD ²

4) SC = BP = N(hauteur )

5) CA 2 +BD 2 = H 2 + UN À 2 + H 2 +PD 2

6) Laisser D K=UN P=x, Alors C ÀD : H 2 = CD 2 - X 2 selon le théorème de Pythagore )

7) AC²+BD ² = CD 2 - x²+ AK 1 ²+ CD 2 -X 2 +PD 2 ,

AC²+BD ²=2СD 2 -2x 2 + UN À 2 +PD 2

8) Un À=AD+ X, R.D=AD- X,

AC²+BD ² =2CD 2 -2x 2 +(ANNONCE +x) 2 +(ANNONCE -X) 2 ,

CA²+ DANSD²=2 AVECD²-2 X² +AD 2 +2AD X+ X 2 +AD 2 -2AD X+ X 2 ,
CA²+ DANSD²=2CD 2 +2AD 2 =2(CD 2 +AD 2 ).

V . Résoudre des problèmes en utilisant ces propriétés

Le point d'intersection des bissectrices de deux angles d'un parallélogramme adjacent à un côté appartient au côté opposé. Le côté le plus court d'un parallélogramme est 5 . Trouvez son grand côté.

Donné: ABCD est un parallélogramme,

AK – bissectrice
UN,

DK – bissectrice
ré , AB = 5

Trouver: Soleil

décision

Solution

Parce que AK - bissectrice
Et puis ABC est isocèle.

Parce que DK – bissectrice
D, alors DCK - isocèle

CC =C K= 5

Alors, BC=VC+SC=5+5 = 10

Réponse : 10

2. Trouvez le périmètre d'un parallélogramme si la bissectrice d'un de ses angles divise le côté du parallélogramme en segments de 7 cm et 14 cm.

1 cas

Donné:
UN,

VK=14 cm, KS=7 cm

Trouver: Parallélogramme P

Solution

VS=VK+KS=14+7=21 (cm)

Parce que AK – bissectrice
Et puis ABC est isocèle.

AB = BK = 14 cm

Alors P=2 (14+21) =70 (cm)

événement

Donné: ABCD est un parallélogramme,

DK – bissectrice
D

VK=14 cm, KS=7 cm

Trouver: P parallélogramme

Solution

VS=VK+KS=14+7=21 (cm)

Parce que DK – bissectrice
D, alors DCK - isocèle

CC =C K= 7

Alors, P = 2 (21+7) = 56 (cm)

Répondre: 70 cm ou 56 cm

3. Les côtés d'un parallélogramme mesurent 10 cm et 3 cm. Les bissectrices de deux angles adjacents au plus grand côté divisent le côté opposé en trois segments. Trouvez ces segments.

1 cas : les bissectrices se coupent à l'extérieur du parallélogramme

Donné: ABCD – parallélogramme, AK – bissectrice
UN,

DK – bissectrice
D , AB = 3 cm, BC = 10 cm

Trouver: VM, MN, NC

Solution

Parce que AM - bissectrice
Et puis AVM est isocèle.

Parce que DN – bissectrice
D, alors DCN - isocèle

DC=CN=3

Alors, MN = 10 – (BM +NC) = 10 – (3+3)=4 cm

Cas 2 : les bissectrices se coupent à l'intérieur d'un parallélogramme

Parce que AN - bissectrice
Et puis ABN est isocèle.

AB = BN = 3 D

Et la grille coulissante doit être déplacée à la distance requise dans l'embrasure de la porte

Mécanisme de parallélogramme- un mécanisme à quatre barres dont les maillons forment un parallélogramme. Il est utilisé pour mettre en œuvre un mouvement de translation par des mécanismes articulés.

Parallélogramme à lien fixe- un maillon est immobile, celui opposé effectue un mouvement de bascule en restant parallèle à celui immobile. Deux parallélogrammes reliés l'un derrière l'autre confèrent au maillon d'extrémité deux degrés de liberté, le laissant parallèle au maillon fixe.

Exemples : essuie-glaces de bus, chariots élévateurs, trépieds, cintres, suspensions de voitures.

Parallélogramme à joint fixe- on utilise la propriété d'un parallélogramme de maintenir un rapport constant des distances entre trois points. Exemple : pantographe à dessin - un appareil pour mettre des dessins à l'échelle.

Rhombe- tous les maillons ont la même longueur, le rapprochement (contraction) d'une paire de charnières opposées entraîne l'écartement des deux autres charnières. Tous les liens fonctionnent en compression.

Exemples : cric automobile en forme de losange, pantographe de tramway.

Ciseaux ou Mécanisme en forme de X, aussi connu sous le nom Ciseaux de Nuremberg- version losange - deux maillons reliés au milieu par une charnière. Les avantages du mécanisme sont la compacité et la simplicité, l'inconvénient est la présence de deux paires coulissantes. Deux (ou plusieurs) de ces mécanismes connectés en série forment un ou plusieurs losanges au milieu. Utilisé dans les ascenseurs et les jouets pour enfants.

VII Conclusion

Qui étudie les mathématiques depuis l’enfance ?

il développe l'attention, entraîne son cerveau,

propre volonté, cultive la persévérance

et persévérance dans l'atteinte des objectifs

A. Markouchevitch

Au cours de mes travaux, j'ai prouvé des propriétés supplémentaires du parallélogramme.

J'étais convaincu qu'en utilisant ces propriétés, vous pouvez résoudre les problèmes plus rapidement.

J'ai montré comment ces propriétés sont appliquées à l'aide d'exemples de résolution de problèmes spécifiques.

J'ai beaucoup appris sur le parallélogramme, qui n'est pas dans notre manuel de géométrie

J'étais convaincu que la connaissance de la géométrie est très importante dans la vie à travers des exemples d'application des propriétés d'un parallélogramme.

Le but de mon travail de recherche est atteint.

L'importance des connaissances mathématiques est attestée par le fait qu'un prix a été créé pour celui qui publie un livre sur une personne qui a vécu toute sa vie sans l'aide des mathématiques. Pas une seule personne n’a encore reçu ce prix.

VIII Littérature

Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles deux à deux. La figure suivante montre le parallélogramme ABCD. Il a le côté AB parallèle au côté CD et le côté BC parallèle au côté AD.

Comme vous l’avez peut-être deviné, un parallélogramme est un quadrilatère convexe. Considérons les propriétés de base d'un parallélogramme.

Propriétés d'un parallélogramme

1. Dans un parallélogramme, les angles opposés et les côtés opposés sont égaux. Montrons cette propriété - considérons le parallélogramme présenté dans la figure suivante.

La diagonale BD le divise en deux triangles égaux : ABD et CBD. Ils sont égaux le long du côté BD et des deux angles qui lui sont adjacents, puisque les angles se trouvent transversalement à la sécante BD des droites parallèles BC et AD et AB et CD respectivement. Donc AB = CD et
avant JC = après JC. Et de l'égalité des angles 1, 2, 3 et 4 il résulte que l'angle A = angle1 + angle3 = angle2 + angle4 = angle C.

2. Les diagonales d'un parallélogramme sont divisées en deux par le point d'intersection. Soit le point O le point d'intersection des diagonales AC et BD du parallélogramme ABCD.

Alors le triangle AOB et le triangle COD sont égaux entre eux, le long du côté et de deux angles adjacents. (AB = CD puisque ce sont des côtés opposés du parallélogramme. Et angle1 = angle2 et angle3 = angle4 sont comme des angles transversaux lorsque les droites AB et CD coupent respectivement les sécantes AC et BD.) Il s'ensuit que AO = OC et OB = OD, ce qui devait être prouvé.

Toutes les propriétés principales sont illustrées dans les trois figures suivantes.

Notion de parallélogramme

Définition 1

Parallélogramme est un quadrilatère dont les côtés opposés sont parallèles entre eux (Fig. 1).

Image 1.

Un parallélogramme a deux propriétés principales. Considérons-les sans preuve.

Propriété 1 : Les côtés et angles opposés d’un parallélogramme sont respectivement égaux.

Propriété 2 : Les diagonales tracées dans un parallélogramme sont divisées en deux par leur point d'intersection.

Signes d'un parallélogramme

Considérons trois caractéristiques d'un parallélogramme et présentons-les sous forme de théorèmes.

Théorème 1

Si deux côtés d’un quadrilatère sont égaux et parallèles, alors ce quadrilatère sera un parallélogramme.

Preuve.

Donnons-nous un quadrilatère $ABCD$. Dans lequel $AB||CD$ et $AB=CD$ Dessinons-y une diagonale $AC$ (Fig. 2).

Figure 2.

Considérons les droites parallèles $AB$ et $CD$ et leur sécante $AC$. Alors

\[\angle CAB=\angle DCA\]

comme des coins entrecroisés.

D'après le critère $I$ d'égalité des triangles,

puisque $AC$ est leur côté commun, et $AB=CD$ par condition. Moyens

\[\angle DAC=\angle ACB\]

Considérons les droites $AD$ et $CB$ et leur sécante $AC$ ; par la dernière égalité entre les angles couchés, nous obtenons que $AD||CB$.) Par conséquent, par définition $1$, ce quadrilatère est un parallélogramme.

Le théorème est prouvé.

Théorème 2

Si les côtés opposés d’un quadrilatère sont égaux, alors c’est un parallélogramme.

Preuve.

Donnons-nous un quadrilatère $ABCD$. Dans lequel $AD=BC$ et $AB=CD$. Dessinons-y une diagonale $AC$ (Fig. 3).

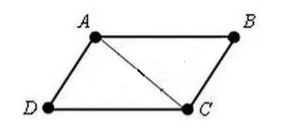
Figure 3.

Puisque $AD=BC$, $AB=CD$ et $AC$ sont un côté commun, alors par le critère $III$ pour l'égalité des triangles,

\[\triangle DAC=\triangle ACB\]

\[\angle DAC=\angle ACB\]

Considérons les droites $AD$ et $CB$ et leur sécante $AC$ ; par la dernière égalité entre les angles couchés, nous obtenons que $AD||CB$. Donc, par définition $1$, ce quadrilatère est un parallélogramme.

\[\angle DCA=\angle CAB\]

Considérons les droites $AB$ et $CD$ et leur sécante $AC$ ; par la dernière égalité entre les angles couchés, nous obtenons que $AB||CD$. Par conséquent, d’après la définition 1, ce quadrilatère est un parallélogramme.

Le théorème est prouvé.

Théorème 3

Si les diagonales tracées dans un quadrilatère sont divisées en deux parties égales par leur point d'intersection, alors ce quadrilatère est un parallélogramme.

Preuve.

Donnons-nous un quadrilatère $ABCD$. Dessinons-y les diagonales $AC$ et $BD$. Laissez-les se croiser au point $O$ (Fig. 4).

Graphique 4.

Puisque, par condition, $BO=OD,\ AO=OC$, et les angles $\angle COB=\angle DOA$ sont verticaux, alors, par le critère $I$ d'égalité des triangles,

\[\triangle BOC=\triangle AOD\]

\[\angle DBC=\angle BDA\]

Considérons les droites $BC$ et $AD$ et leur sécante $BD$ ; par la dernière égalité entre les angles couchés, nous obtenons que $BC||AD$. Aussi $BC=AD$. Donc, d'après le théorème $1$, ce quadrilatère est un parallélogramme.